Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 98
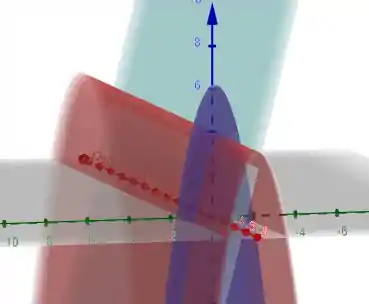
O paraboloide intercepta o plano em uma parábola. Determine as equações paramétricas para a reta tangente a essa parábola no ponto . Use um computador para fazer o gráfico do paraboloide, da parábola e da reta tangente em uma mesma tela.
Passo 1
Fala a pessoal! Vamos resolver um questãozinha juntos?
Seguinte! O enunciado pede para determinar as equações paramétricas para a reta tangente à parábola resultante da interseção do paraboloide com o plano , no ponto .
Para resolver, vamos precisar:
- Encontrar a equação da parábola resultante da interseção do paraboloide e do plano.
- Calcular o vetor normal à superfície nesse ponto.
- Usar o vetor normal e o ponto dado para encontrar a equação da reta tangente.
Eai?! Entendeu o passo a passo?
Agora é só resolver!
Passo 2
Primeiramente, galera, precisamos determinar qual é a equação da parábola supracitada pelo enunciado. Como o paraboloide intercepta o plano em , se substituirmos esse valor na equação que nos foi dada, obteremos:
Para encontrarmos a reta tangente à essa parábola no ponto específicado, basta derivarmos parcialmente a função em relação a e substituir o ponto dado, saca só:
Temos que
Passo 3
Tudo bem, já encontramos a reta tangente à parábola no ponto indicado. Agora nos resta descobrirmos as equações paramétricas para a reta tangente. Para as três dimensões, temos que o formato das equações serão:
Os valores de e nós temos, então basta descobrirmos e , certo? Assim como o enunciado nos diz, é constante, então . O valor de nós descobrimos implicitamente no passo anterior, vale . Por fim, o valor de é . Sendo assim, nossas equações serão:
Passo 4
Plotando o gráfico das funções, teremos:
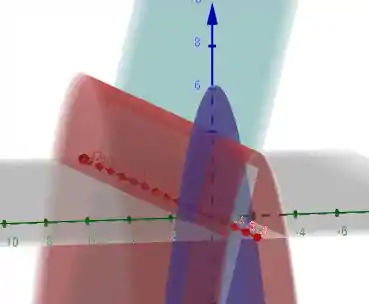
No qual em roxo está o paraboloide, em vermelho está a parábola e em azul claro está a reta tangente.
Resposta
