Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 92
Se a, b e c são os lados de um triângulo e A, B e C são os ângulos opostos, determine pela derivação implícita da Lei dos Cossenos.
Passo 1
E aí, galera! Beleza?
Bom, nessa questão nós temos um triângulo, seus lados e ângulos. A questão nos pede para determinar algumas derivadas pela derivação da lei dos Cossenos.
Imaginemos um triângulo qualquer conforme o indicado na figura abaixo:
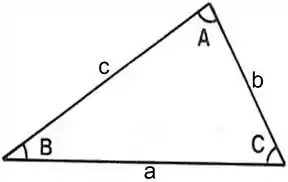
Pela Lei dos Cossenos,
De modo que, para calcularmos aquelas derivadas do enunciado, precisamos derivar implicitamente essa Lei dos Cossenos com relação aos lados.
A derivação implícita consiste em assumir que todos os parâmetros da equação dependem uns dos outros.
Vamos ver como fica isso na prática?
Passo 2
Vamos derivar implicitamente a lei dos Cossenos em relação a :
Aqui vamos precisar usar a regra do produto, pois temos, por hipótese, três funções de .
Vale chamar a atenção que:
Juntando isso à regra do produto,
Substituindo esse resultado na derivação da lei dos cossenos, temos:
Queremos calcular , então precisamos isolá-lo na equação acima:
Passo 3
De maneira semelhante, derivando em relação a :
Agora queremos
Passo 4
Por último, derivando em relação a :
Isolando :