As populações de pulgões e joaninhas são modeladas pelas equações
- Calcule as soluções de equilíbrio e explique seu significado.
- Encontre uma expressão para
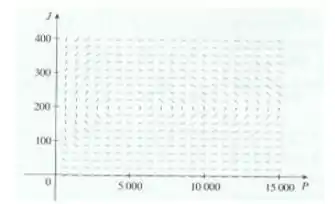
- O campo de direções para a equação diferencial na parte (b) é mostrado. Use-o para esboçar um retrato de fase. O que as trajetórias de fase têm em comum?
- Suponha que no instante existam pulgões e joaninhas. Desenhe a trajetória de fase correspondente e use-a para descrever como as populações variam.
- Use a parte (d) para fazer esboços das populações de pulgões e joaninhas como fuções de . Como os gráficos estão relacionados?
Passo 1
- Queremos encontrar as soluções de equilíbrio para as equações
- Agora precisamos encontrar uma expressão que nos forneça a variação da quantidade de joaninhas com relação aos pulgões, ou seja, queremos encontrar .
- Queremos usar o campo de direções dado para esboçar um retrato de fase, para isso, basta pegar o campo e traçar várias curvas acompanhando as direções. Assim,
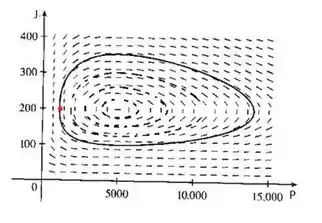
- Suponha que no instante existam pulgões e joaninhas. Queremos desenhar a trajetória de fase correspondente e usá-la para descrever como as populações variam.
- Agora, nós queremos usar o gráfico do item (d) para fazer o gráfico das populações ao passar do tempo. Ao interpretar os números da curva, ficamos com o seguinte gráfico:
Uma solução de equilíbrio acontece quando a derivada da função é igual a . Então se e são constantes, , e , olhando para a segunda equação, ficamos com:
Então Portanto, é uma solução de equilíbrio.
Por outro lado, se :
Quando e for uma constante, temos:
Então outra solução de equilíbrio é
Passo 2
Bom, para encontrar isso, podemos fazer x
x
Passo 3
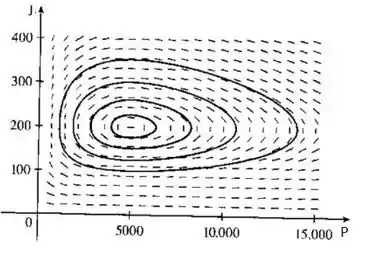
O que podemos perceber é que o ponto de equilíbrio, está dentro de todas as trajetórias de fase.
Passo 4
Bom, assim como no item (c), basta pegarmos o campo de direções, marcar o ponto inicial , e traçar uma curva seguindo as direções.
Passo 5
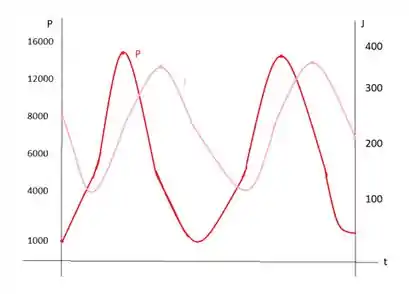
A relação que podemos observar entre as duas curvas é que o período de repetição entre elas é o mesmo
Resposta
- e