Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 23
A posição de determinado oscilador ligeiramente amortecido satisfaz o problema de valor
Inicial
Note que, exceto pelo termo de amortecimento, esse problema é igual ao Problema 18.
a) Tente prever a natureza da solução sem resolver o problema.
b) Teste sua previsão encontrando a solução e desenhando seu gráfico.
c) Determine o que acontece após o final da sequência de impulsos.
Passo 1
a) bem vamos tentar prever a solução sem resolver. Nós poderíamos calcular a Laplace inversa da função na nona forma da tabela 6.2.1, oque teria criado uma exponencial com fatores e expoentes negativos na solução. Isto provavelmente mudaria a amplitude da solução do problema 18 e gradualmente iria diminuindo e aumentando sua amplitude, após certo valor de t.
Passo 2
b) Pela transformada de Laplace do lado esquerdo nós teremos a equação no domínio de , e de acordo com a linearidade da tabela de Laplace 6.2.2.
Bem utilizando os calculas que já foram feitos na questão 18, temos que o lado direito da nossa igualdade é:
Igualando as duas equações temos:
Simplificando temos:
Utilizando a tabela 6.2.1 e olhando os itens 9 e 13, para aplicarmos a transformada inversa de Laplace, temos:
Passo 3
c) Aplicando a função que acabamos de calcular, teremos o seguinte gráfico:
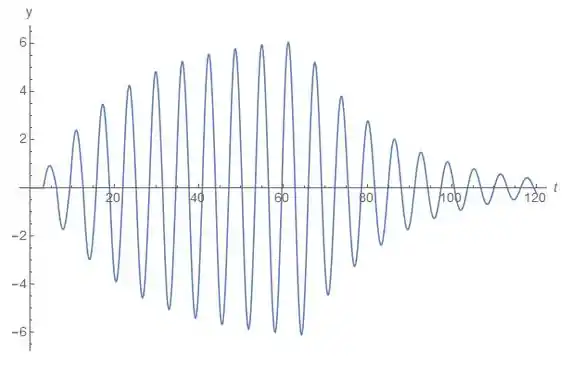
Após a sequencia de pulso terminar, a função continua sendo uma função oscilatória, mas cada vez mais com uma amplitude diminuindo.
Resposta
b)
c) Após a sequencia de pulso terminar, a função continua sendo uma função oscilatória, mas cada vez mais com uma amplitude diminuindo.