Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 20
Os problemas de 17 a 22 tratam do efeito de uma sequência de impulsos aplicados em um oscilador não amortecido. Suponha que
Para cada uma das escolhas para :
(a) Tente prever a natureza da solução sem resolver o problema.
(b) Teste sua previsão encontrando a solução e desenhando seu gráfico.
(c) Determine o que acontece após o final da sequência de impulsos.
20)
Passo 1
a) Baseado na solução do problema 16(b) desta mesma seção, podemos prever que a solução será da seguinte forma:
Devido a linearidade da transformada inversa de Laplace.
Passo 2
b) Pela transformada de Laplace e aplicando na equação diferencial:
Nós temos equação de Laplace do lado esquerdo e podemos coletar a transformada do lado direito pela seguinte equação:
Bem igualando o resultado das duas equações que calculamos temos:
Ou
Aplicando a transformada inversa de Laplace, olhando nos itens 5 e 13, da tabela 6.2.1, temos:
Passo 3
c)Utilizando nossas equações para plotar o gráfico temos:
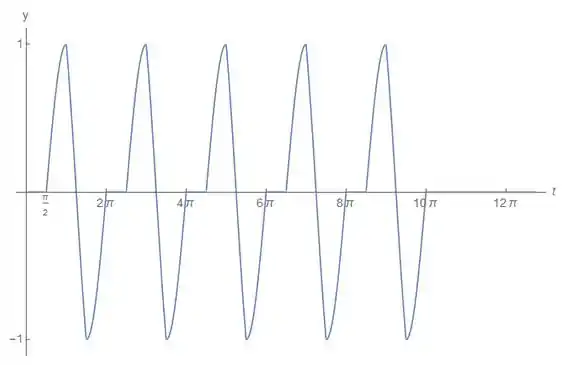
Perceba que após uma sequencia de pulsos terminar, a solução fica qual a zero.
Resposta
a)
b)
c) Perceba que após uma sequencia de pulsos terminar, a solução fica igual a zero.