Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 24

Proceda como no Problema 23 para o oscilador satisfazendo

y ' ' + 0,1 y ' + y = ∑ k = 1 15 δ t - 2 k - 1 π ,       y 0 = 0 ,     y ' 0 = 0 .

Note que, exceto pelo termo de amortecimento, esse problema é igual ao Problema 21.

Passo 1

a) bem vamos tentar prever a solução sem resolver. Nós poderíamos calcular a Laplace inversa da função na nona forma da tabela 6.2.1, oque teria criado uma exponencial com fatores e expoentes negativos na solução. Isto provavelmente mudaria a amplitude da solução do problema 18 e gradualmente iria diminuindo t e aumentando sua amplitude, após certo valor de t.

Passo 2

Bem, para prosseguirmos aqui, para calcularmos o lado esquerdo da nossa transformada de Laplace já foi efetuado no problema 23, portanto vamos importa-la de lá que é:

= s 2 + 0,1 s + 1 Y s

E o lado direito da nossa equação foi calculado no problema 21, e também iremos importar de lá:

∑ k = 1 20 e - - 2 k - 1 π s

Agora que temos os dois lados vamos igualar as funções:

s 2 + 0,1 s + 1 Y s = ∑ k = 1 20 e - - 2 k - 1 π s

Y s = ∑ k = 1 20 e - - 2 k - 1 π s s 2 + 0,1 s + 1 = ∑ k = 1 20 e - - 2 k - 1 π s s + 1 20 2 + 399 400

Y s = ∑ k = 1 20 20 399 e - - 2 k - 1 π s   399 20     s + 1 20 2 + 399 400

Aplicando a transformada inversa de Laplace, olhando nos itens 5 e 13, da tabela 6.2.1, temos:

y = ∑ k = 1 20 20 399 u 2 k - 1 π t e - t - 2 k - 1 π 20   s e n   399 t - 2 k - 1 π 20

Passo 3

c) Escrevendo a função, temos o seguinte gráfico:

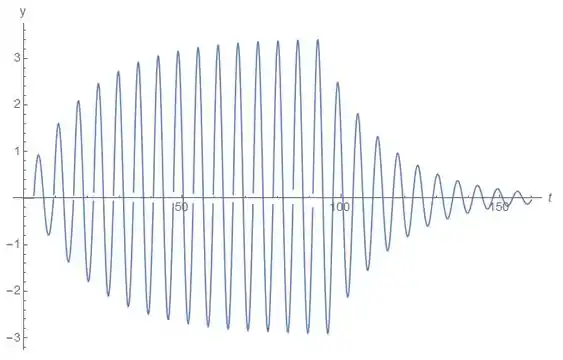
Após a sequencia de pulso terminar, a função continua sendo uma função oscilatória, mas cada vez mais com uma amplitude diminuindo.

Resposta

b) y = ∑ k = 1 20 20 399 u 2 k - 1 π t e - t - 2 k - 1 π 20   s e n   399 t - 2 k - 1 π 20

c) Após a sequencia de pulso terminar, a função continua sendo uma função oscilatória, mas cada vez mais com uma amplitude diminuindo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os problemas de 17 a 22 tratam do efeito de uma sequência de impulsos aplicados em um oscilador não amortecido. Suponha que y ″+y=f( t ) ,y ( 0 )=0 ,y '( 0 )=0 . Para cada uma das escolhas para f ( t
Os problemas de 17 a 22 tratam do efeito de uma sequência de impulsos aplicados em um oscilador não amortecido. Suponha que y ″+y=f( t ) ,y ( 0 )=0 ,y '( 0 )=0 . Para cada uma das escolhas para f ( t
Considere o problema de valor inicial y ″+y=f k( t ) ,y ( 0 )=0 ,y '( 0 )=0 , em que f k ( t )=[ u 4 – k ( t )–u 4 + k ( t ) ] / 2 k com 0k≤1 .(a) Encontre a solução y=ϕ ( t ,k ) do problema de valor
Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.13. y ' ' - 2 y ' + 2 y = 0 ; y 0 = 0 ; y ' 0 = 1
Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.11. y ' ' - y ' - 6 y = 0 ; y 0 = 1 , y ' 0 = - 1