Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 1b
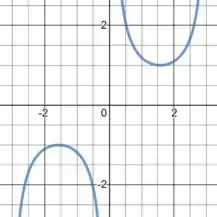
Determine o domínio e esboce o gráfico.
Passo 1
Como sabemos que
Então:
Como temos uma divisão de duas funções e
Passo 2
Como temos uma divisão de duas funções e não existe divisão por zero, sabemos que o denominador não pode ser zero.
Assim o domínio é:
Passo 3
E o seu gráfico é dado por:
Resposta
Exercícios de Livros Relacionados
Explique porque a função é descontínua no número dado a . Desenho o gráfico da função.
Prove, sem usar gráficos, que o gráfico da função tem pelo menos dois pontos interceptando o eixo x no intervalo especificado.
Use o teorema do valor intermediário para mostrar que existe uma raiz no intervalo especificado para a equação dada.
Use a definição de continuidade e as propriedades dos limites para mostrar que a função é contínua no intervalo dado. f x = x + x - 4 4 , ∞ .
Explique, usando os teoremas 4, 5, 7 e 9, porque a função é contínua para qualquer número em seu domínio. Explicite o domínio.