Uma região é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva como uma integral iterada, onde é uma função qualquer contínua em .
Passo 1
Faaala minha turminha? Vamos analisar essa questão.
Ele fornece uma região , e pediu para decidir se a integral abaixo será escrita em coordenadas polares ou retangular. Lembre-se que uma integral iterada, é uma integral com limites de integração.
Observe a região R fornecida, ela tem a cara de um semicírculo de raio 1. Certo?
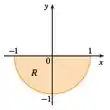
Lembre-se, para o círculo, torna-se mais cômodo utilizar coordenadas polares. Em coordenadas polares, temos que:
Portanto, agora sabemos a expressão do círculo e como escrever x e y em coordenadas polares. Como é um semicírculo, o ângulo varia no sentido anti-horário entre:
Temos que o raio varia:
Com esse bizu, vocês vão gabaritar! Bora lá resolver juntos!
Passo 2
Bom, vamos lá.
Queremos representar a integral dupla como uma integral iterada.
A região , em coordendas polares temos:
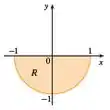
Onde:
Logo, aplicando na integral. Vamos ter: