Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 13i
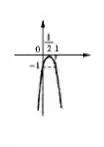
Com relação à função dada, determine a raízes (caso existam), o maior ou o menor valor e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vou ajudar vocês nessa questão. Bora lá? Bom, a é uma função de segunda ordem, portanto a cara dela é de uma parábola. E para desenhar, precisamos de quatro pontos:
- As duas raízes (onde o gráfico corta o eixo );
- O ponto do termo independente (onde o gráfico corta o eixo )
- E o vértice: que mostra onde o gráfico vai apresentar o valor máximo (se a parábola tiver boca para baixo ) ou um mínimo (se a parábola tiver boca para cima ).
Então vamos aos pontos?
Passo 2
Vamos achar as raízes da função:
Usando a fórmula de Bhaskara temos:
Então as duas raízes (nesse caso idênticas) são:
E já vou aproveitar e determinar onde a função corta o eixo vertical: :
Certo! Achamos o ponto .
Passo 3
Por fim, vamos ao vértice. A coordenada do vértice é então:
E a coordenada é dada por :
Perfeito! O outro ponto é . Como essa parábola tem , ela tem boca para baixo, então o do vértice representa o valor máximo que ela pode assumir.
O maior valor que a parábola assume é:
Passo 4
Relembrando:
- Raiz:
- Ponto onde corta o eixo :
- Vértice (máximo):
Agora é só esboçar o gráfico:
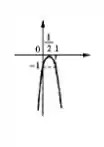
Resposta
