Representar graficamente os seguintes subconjuntos de . Identificar os conjuntos abertos.
Passo 1
Galera, pra gente representar graficamente o conjunto, primeiro vamos dar uma ajeitada na equação dele, porque assim não dá pra concluir nada! O conjunto é:
Então vamos mexer na equação:
Isolando o , vamos ficar com:
Isso quer dizer que queremos o espaço abaixo dessa reta, contando com ela, por causa do sinal de igual! Por ter essa borda marcada por ela, o conjunto não é aberto.
Passo 2
Representando graficamente:
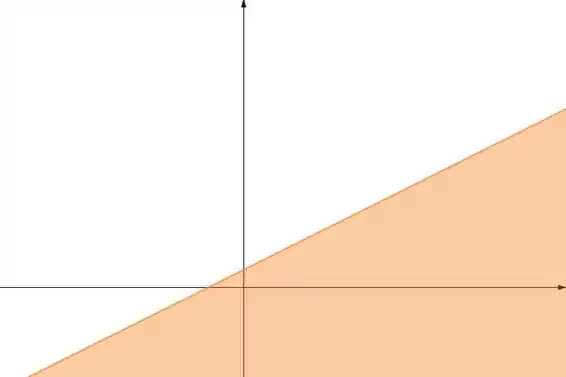
Resposta
Região abaixo de uma reta, contando com ela. O conjunto não é aberto.