Represente graficamente o domínio da função dada por:
Passo 1
Aplicar as condições do problema:
Apenas teremos quando:
Passo 2
Representar graficamente a equação encontrada:
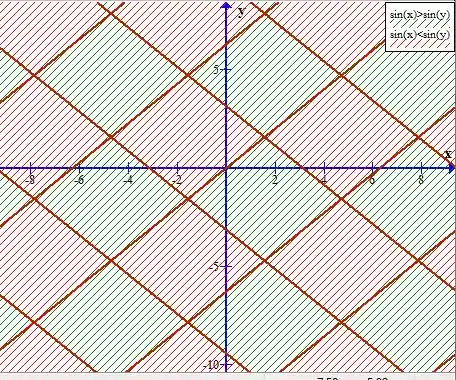
Represente graficamente o domínio da função dada por:
Aplicar as condições do problema:
Apenas teremos quando:
Representar graficamente a equação encontrada:
