Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.1 - Ex. 3e
Represente graficamente e o domínio da função dada por
e)
Passo 1
Vamos isolar da equação para tornar uma função de e .
Isolando, temos que
Ou, seja
Como , vamos considerar apenas
Passo 2
Agora, vamos analisar o domínio, ou seja, para quais valores não temos problema em aplicar a função.
Para que a função em e), para valores reais não tenha problema, precisamos que o que está dentro da raiz seja positivo, isto é,
Arrumando as contas,
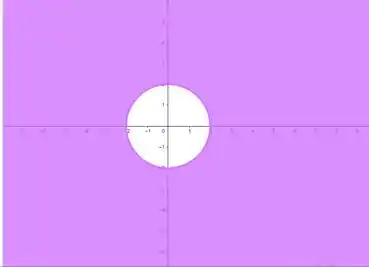
Geometricamente, temos a região fora do círculo de centro na origem e raio 2.
Resposta
Exercícios de Livros Relacionados
Represente graficamente e o domínio da função z = f x , y dada por h) z = x - y s e n x - s e n y
Represente graficamente e o domínio da função z = f x , y dada por d) z = ln 2 x 2 + y 2 - 1
Represente graficamente e o domínio da função z = f x , y dada por f) z = x - | y |
Verifique se a função é homogênea .Em caso afirmativo, determine o grau de homogeneidade. d) f ( x , y ) = 2 x 2 + y 2
Represente graficamente e o domínio da função z = f x , y dada por b) f x , y = x - y 1 - x 2 - y 2