Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.1 - Ex. 3 d
Represente graficamente e o domínio da função dada por
d)
Passo 1
Vamos analisar o domínio, ou seja, para quais valores não temos problema em aplicar a função.
Para que a função do enunciado não tenha problema precisamos que o que está dentro do seja maior que zero, ou seja
Arrumando as contas,
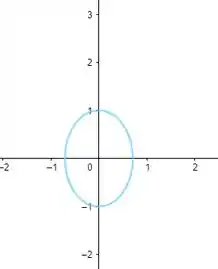
Geometricamente, temos a região de fora de uma elipse de eixo maior no eixo y e menor no eixo .
Resposta
Exercícios de Livros Relacionados
Um modelo para a área da superfície de um corpo humano é dado pela função S = f w , h = 0,1091w 0,425h 0,725 onde w é o peso (em libras), h é a altura (em polegadas) e S é medida em pés quadrados.a) E
Um fabricante modelou sua função P da produção anual (o valor monetário de toda a produção em milhões de dólares) como uma função de Cobb-Douglas P L ,K = 1,47L 0,65 K 0,35 onde L é o número de horas
Uma empresa fabrica caixas de papelão de três tamanhos: pequena, média e grande. O custo é de $ 2,50 para fabricar uma caixa pequena, $ 4,00 para uma caixa média e $ 4,50 para uma caixa grande. Os cus
Seja g x , y , z = x 3 y 2 z 10 - x - y - z .Calcule g ( 1,2 , 3 ) .Determine o domínio de g .
Seja F x , y = 1 + 4 - y 2 . Calcule F ( 3,1 ) .Determine e esboce o domínio de F . Determine a imagem de F .