Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.1 - Ex. 3 h
Represente graficamente e o domínio da função dada por
h)
Passo 1
Vamos analisar o domínio, ou seja, para quais valores não temos problema em aplicar a função.
Para que a função em h), para valores reais não tenha problema, precisamos que o que está no denominador seja sempre não nulo, ou seja
Reescrevendo
O que significa dizer que
E
Com .
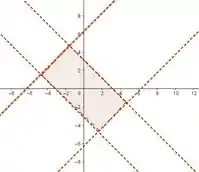
Geometricamente, temos que o domínio corresponde a região entre as retas e (as retas pontilhadas não entram.)
Resposta
Exercícios de Livros Relacionados
Verifique se a função é homogênea .Em caso afirmativo, determine o grau de homogeneidade. d) f ( x , y ) = 2 x 2 + y 2
Represente graficamente e o domínio da função z = f x , y dada por b) f x , y = x - y 1 - x 2 - y 2
Represente graficamente e o domínio da função z = f x , y dada por c) z = y - x 2 + 2 x - y
Represente graficamente e o domínio da função z = f x , y dada por g) 4 x 2 + y 2 + z 2 = 1
Represente graficamente e o domínio da função z = f x , y dada por x + y - 1 + z 2 = 0 ,z ≥ 0