Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 46
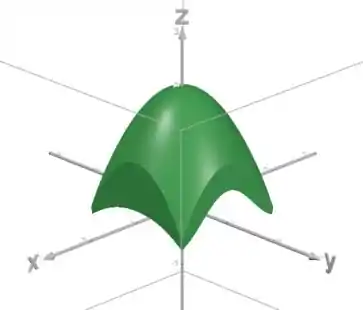
Represente graficamente o sólido que se encontra entre a superfície e para , . Use um sistema algébrico computacional para aproximar o volume do sólido para quatro casas decimais.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Ela ta pedindo duas coisas pra gente:
- Representar o sólido que ele definiu na questão em um gráfico
- Aproximar o volume do sólido em quatro casas decimais usando um software
Então vamos fazer por partes!
Passo 2
Primeiro, plotamos as superfícies dadas no enunciado.
Vamos usar duas funções:
Além disso, essas funções estão limitadas por:
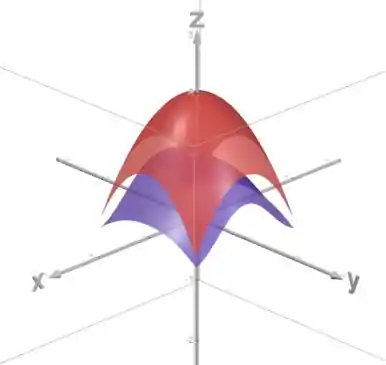
A função está em roxo e a em vermelho.
Assim, o sólido delimitado por essas superfícies fica:
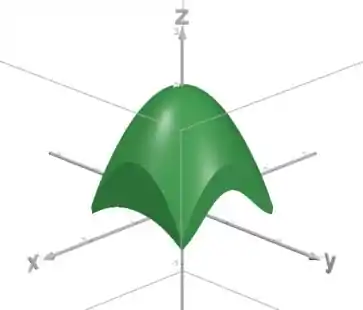
Passo 3
Como podemos observar, a função que chamamos é maior do que a em toda a região que estamos trabalhando.
Ou seja, para calcularmos o volume desse sólido, teremos que calcular a integral de :
A região é definida pelas limitações em e :
Então,
Agora calculamos usando ajuda de software – vou usar o WolframAlpha.
Entrada:
Resposta:
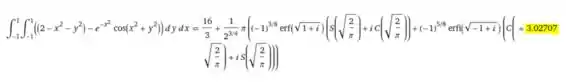
Ou seja,
Resposta
