Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 32
A resistividade de um fio condutor é o recíproco da condutividade e é medida em unidades de ohm-metros (). A resistividade de um dado metal depende da temperatura de acordo com a equação
Onde é a temperatura em . Existem tabelas que listam os valores de (o coeficiente de temperatura) e (a resistividade a ) para vários metais. Exceto a temperaturas muito baixas, a resistividade varia quase linearmente com a temperatura, e assim é comum aproximar a expressão para por seu polinômio de Taylor de grau 1 ou 2 em .
- Encontre expressões para estas aproximações linear e quadrática.
- Para o cobre, a tabela fornece e . Trace a resistividade do cobre e as aproximações linear e quadrática para .
- Para quais valores de a aproximação linear coincide com a expressão exponencial com precisão de ?
Passo 1
E aí, galerinha! Tudo certo?
Nossa questão aqui tem 3 partes:
A parte a) pede que a gente encontre expressões para a aproximação linear e quadrática da resistividade em relação a temperatura. Como o próprio enunciado diz, essa relação é dada pela função:
E é podemos achar uma aproximação pra essa função através do polinômio de Taylor de grau 1 ou 2 em .
A aproximação linear é dada pelo polinômio de Taylor de grau 1:
E a aproximação quadrática é dada pelo polinômio de Taylor de grau 2:
Então, o que precisamos fazer é encontrar o valor das derivadas e da nossa função e substituirmos na nossa equação acima.
A parte b) quer os gráficos dos polinômios que encontramos com os valores dados no enunciado.
Por fim, a parte c) quer saber qual intervalo de valores de apresenta uma precisão, ou seja, um erro de até entre a função original e sua aproximação por :
Ou seja, valores de que apresenta diferença máxima da função original de , para mais ou para menos. Nós achamos esse intervalo pelo gráfico da função e dos polinômios.
Vamos por isso em prática.
Passo 2
A primeira coisa que temos que fazer é encontrarmos os valores da primeira derivada e da segunda derivada da função para aplicarmos nas equações de e , assim como .
Nossa função original é:
Derivando uma vez:
Derivando uma segunda vez:
Agora temos que achar essas derivadas e a função original no ponto que o enunciado deu :
Substituindo :
Na função original:
Na primeira derivada:
Na segunda derivada:
Como
esse termo “some”.
Passo 3
Agora podemos substituir os valores que encontramos: O polinômio de Taylor de grau 1 (ou aproximação linear da função) será:
Fazendo:
E:
Teremos:
O polinômio de Taylor de grau 2 (ou aproximação quadrática da função) será:
Substituindo:
E:
Temos em fim:
Colocando a constante em evidência:
Pronto, polinômios de Taylor de grau 1 e 2 encontrados!
Passo 4
Substituindo e nas expressões da resistividade e da aproximação linear e quadrática que encontramos:
Na função original:
Na aproximação por polinômio de grau 1 (linear):
E de grau 2 (quadrática):
Portanto, precisamos plotar essas três curvas aí. Usando uma ferramenta gráfica, como a própria questão sugere, digitamos essas três funções de e obtemos as seguintes curvas:
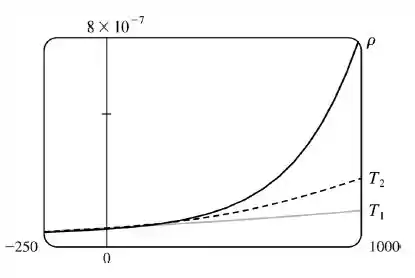
Repare que nas proximidades de aproxima linearmente a curva exponencial de e aproxima na forma quadrática, sendo uma aproximação mais aproximada que a aproximação linear haha quer dizer, uma aproximação um pouquinho mais próximo do real.
Passo 5
Aqui, precisamos achar qual intervalo de valores de apresenta uma precisão, ou seja, um erro de até entre a função original e sua aproximação por :
Se queremos ter uma precisão de , queremos ter algo em torno de:
Somando os valores nas extremidades da inequação:
Beleza, agora vamos dar um zoomzãaaaao no gráfico procurando nesse intervalo.
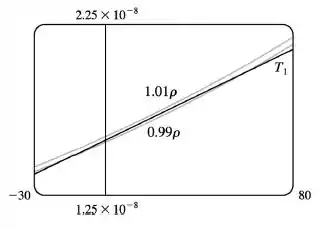
Fazendo isso, vamos que está nesse intervalo quando .
Resposta
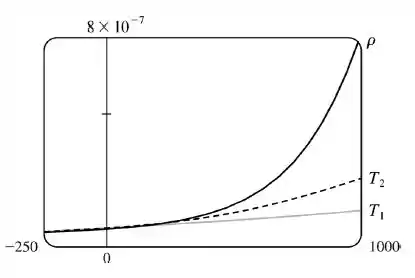
está em quando .