Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.2 - Ex. 23

23. Resolva o problema de valor inicial y ' =   2 y 2   +   x y 2 ,

  y ( 0 )   =   1

e determine onde a solução atinge seu valor mínimo.

Passo 1

Temos aqui o iniciozinho de equações diferenciais, e para resolver essa equação vamos precisar usar um método poderoso de resolução de equações. O método de Separação de Variáveis. O próprio nome já dá spoiler de como funciona. Vamos separar as variáveis, tudo que for x fica de um lado, tudo que for y fica do outro.

Passo 2

No caso de

y ' =   2 y 2   +   x y 2

Podemos fazer o seguinte

y ' = y 2 2 + x

d y d x =   y 2 2 + x  

1 y 2 d y = 2 + x d x

- 1 y = 2 x + x 2 2 + C

Não se esqueça da constante arbitrária ( C ), ela é muito importante !!!

Passo 3

Vamos resolver o problema de valor inicial

y 0 =   1

Dessa forma, temos

- 1 y = 2 x + x 2 2 + C

- 1 1 = C

C =   - 1

Ajeitando essa equação temos

y =   - 2 4 x + x 2 - 2

Passo 4

O enunciado pergunta se essa equação possui um mínimo. Bem primeiro vamos ter que olhar para o gráfico dela

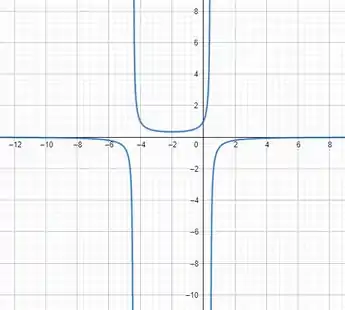
Temos um problema com o domínio em dois pontos, e a equação diverge para ±   ∞ nesse ponto, logo não teremos nem um máximo nem um mínimo global. Teremos apenas um mínimo local, ali no ponto x =   - 2   como podemos ver pelo gráfico. Podemos provar isso algebricamente. Os pontos críticos são onde a derivada da nossa função é nula, assim

y ' = 0

y 2 2 + x =   0

Logo teremos

y = 0   ou x = - 2

Podemos descartar y = 0 porque está fora do nosso domínio, afinal se y = 0

y =   - 2 4 x + x 2 - 2

4 x + x 2 - 2 =   ∞ → x = ∞

Portanto nossa resposta é

x = - 2

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

y =   - 2 4 x + x 2 - 2

Mínimo Local em

x =   - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva a equação diferencial x y ' = y + x e y x usando a mudança de variáveis v = y x .
(a) Resolva a equação diferencial y ' = 2 x 1 - y 2. (b) Resolva o problema de valor inicial y ' = 2 x 1 - y 2 , y 0 = 0 e faça um gráfico da solução.(c) O problema de valor inicial y ' = 2 x 1 - y 2
Resolva a equação e - y y ' + c o s x = 0 e trace vários membros da família de soluções. Como a curva solução muda quando a constante C varia?
Uma solução de glicose é administrada por via intravenosa na corrente sanguínea a uma taxa constante r . À medida que a glicose é adicionada, ela é convertida em outras substâancias e removida da corr
Em uma reação química elementar, as moléculas únicas de dois reagentes A e B formam a molécula do produto C: A + B → C . A lei de ação das massas afirma que a taxa de reação é proporcional ao produto