Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 63
Resolver o exercício supondo que a temperatura seja dada por:
Passo 1
Vamos repetir o que fizemos na anterior. Ele fala sobre a direção em que a temperatura esquenta e diminui o mais rápido possível. Se ele está falando em direção de máximo crescimento (e também máximo crescimento pra diminuir, no caso do resfriamento, só pode estar falando em uma coisa: derivada direcional! A direção de máximo crescimento da temperatura é aquela em que a derivada tem o maior módulo, sacou? Pra calcular a derivada direcional do campo, a primeira coisa que vamos ter que fazer é calcular o gradiente desse campo. Bom, isso a gente sabe fazer, né? Se a nossa função for , o gradiente vai ser dado por:
Aqui a gente não tem , mas tem o , que também é uma função, igualzinho ao hahah Pra facilitar, vamos até dizer que e resolver com essa letra.
Outra coisa, galera: geometricamente, a direção de esquentar e de esfriar mais rapidamente é a mesma, só muda o sentido que ele está andando!
Passo 2
Bora lá! A função é:
Calculando as derivadas parciais:
Assim,
Passo 3
Bom, esse é o gradiente da função:
E esse gradiente é uma função , cujas componentes são as derivadas da trajetória dele em e :
Isso dá um sistema!
Resolvendo,
A partícula estava inicialmente em , e está em , ou seja, em .
Para :
Portanto, a trajetória é dada por:
Então essa trajetória é do tipo . Como o só vai até , então o intervalo da trajetória é , já que ele começa em e vai até . Com isso encontramos a resposta da letra (b)!
Para :
Portanto, a trajetória é dada por:
Então essa trajetória segue a direção de .
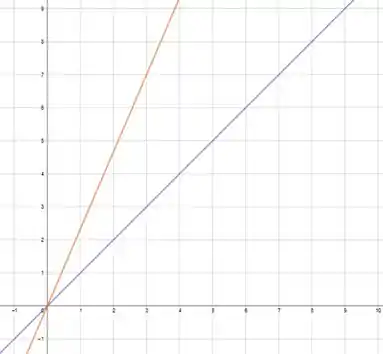
Desenhando as trajetórias, podemos ver que elas não se encontram. Ué, mas e o desenho? Tá se encontrando na origem! Sim, se ele fosse completo, mas não se esquece que o da reta (azul) só começa em , e por isso, não vai passar realmente pela origem.
Resposta
a) Não se encontram.
b)