Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 16c
Para resolver os exercícios e , o aluno deve ter familiaridade com as equações diferenciais lineares de segunda ordem com coeficientes constantes.
Um objeto com vetor posição se move ao longo da parábola . Sabendo que a componente horizontal do vetor aceleração em cada instante é , e que no instante ele se encontra no ponto com vetor velocidade , pede-se:
c) Esboce a trajetória do objeto
Passo 1
Show, olha, todas as questõs pedem pra gente o vetor posição. Então bora lá. Pra começar, veja que:
Do enunciado que diz pra gente a componente horizontal do vetor aceleração, tiramos que:
E olha só! Uma EDO de 2ª ordem com coeficientes constantes! Pra acharmos a solução, escrevemos a equação característica:
Eita! Raizes complexas na equação característica! Sendo assim a solução vai ter essa cara:
Onde:
Logo:
Agora falta determinar essas constantes, pra isso, temos, do enunciado:
Pra achar a outra constante, temos que usar a informação do enunciado:
Isso porque:
E logo:
Derivando:
Feshow a parametrização galera! Se temos:
Basta fazer:
E logo:
Passo 2
Bem, mas não queremos exatamente nessa questão né. Mas precisamos dele pra responder. Pra esboçar, a princípio, como é uma parábola, desenha-la parece o suficiente:
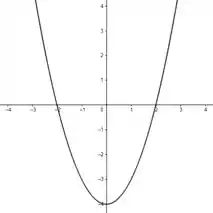
No entanto, note o seguinte:
Como todo boa função seno, temos:
E é a partir dessas duas inequações que vamos tirar informações importantíssimas. Da primeira, tiramamos:
E da segunda, tiramos:
Considerando as restrições de e , conseguimos um esboço mais certinho:
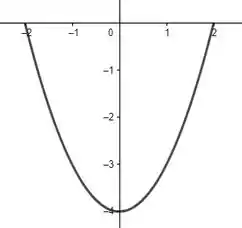
Resposta
