Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 9
As seguintes superfícies, rotuladas , e são gráficos de uma função e de suas derivadas parciais e . Identifique cada superfície e dê razões para sua escolha.
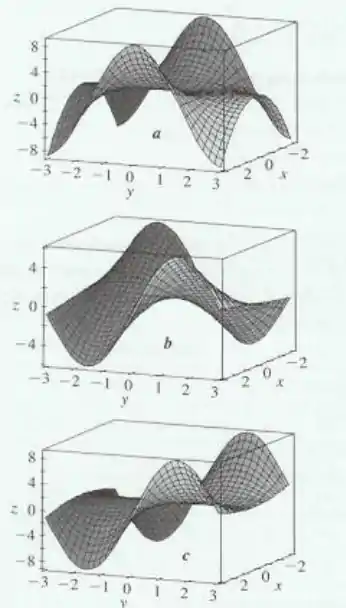
Passo 1
Galera, se a gente começa no ponto e nos movemos no sentido positivo do eixo , a gente nota que ambos e decrescem, enquanto cresce. Além disso, ambos e tem um ponto mínimo perto de , enquanto é nesse ponto. Ou seja, é definitivamente o gráfico de .
Passo 2
Agora, para ver qual entre e é ou , vamos começar no ponto e nos mover no sentido positivo do eixo . Repare que traça uma reta com inclinação negativa, enquanto traça uma parábola com concavidade para baixo. Isso nos diz que é o gráfico de e é o gráfico de .
Resposta
Exercícios de Livros Relacionados
Curvas normais Uma curva lisa é normal a uma superfícieƒ(x, y, z) = c em um ponto de interseção se o vetor velocidade da curva é um múltiplo escalar diferente de zero de §ƒ noponto.Mostre que a curvar
Encontre três números positivos cuja soma seja 3 e cujo produto seja um máximo.
Encontre a distância mínima entre o ponto (2, –1, 1) e o planox + y – z = 2.
Encontre a distância mínima entre o cone z = 2x2 + y 2 e oponto (– 6, 4, 0).
Encontre três números cuja soma seja 9 e cuja soma de quadrados seja um mínimo.