Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.4 - Ex. 7
A seguir é dada uma função em um intervalo de comprimento . Em cada caso, esboce os gráficos da extensão par e da extensão ímpar de de período .
Passo 1
Nosso primeiro passo para resolver o exercício é relembrar o conceito de função par e função ímpar.
Uma função par é uma equação em que:
Para todo contido no domínio de .
Por outro lado, uma função ímpar é definida como:
Para todo contido no domínio de .
Com estes conceitos em mente, vamos analisar se a função dada é par, ímpar ou nenhuma das duas. Tudo bem?
Passo 2
O exercício nos pede para esboçar as extensões par e ímpar da função. Mas antes, vamos determinar qual parte da função é par ou ímpar. No intervalo ,
Se aplicarmos a função para um valor , em que é um valor arbitrário dentro do domínio do intervalo :
Se aplicarmos agora para :
Então
Portanto, é ímpar.
Para o intervalo :
Se aplicarmos a função para um valor , em que é um valor arbitrário dentro do domínio do intervalo :
Se aplicarmos agora para :
Então
Portanto, é par.
Passo 3
Agora que já observamos os intervalos em que a função é par ou ímpar, podemos graficar cada extensão em um intervalo . Primeiro, vamos esboçar toda a função :
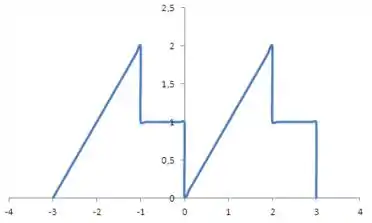
Sendo que corresponde à extensão par da função :
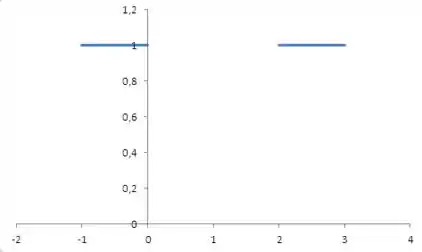
A extensão ímpar da função no intervalo :
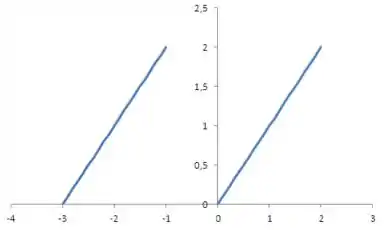
Resposta
Ei, a resposta está no passo a passo :)