Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 2

2. Seja F um campo vetorial de classe C1 no aberto Ω. Sejam σ1 e σ2 porções de superfícies regulares com fronteiras Γ1 e Γ2 orientadas positivamente com relação às normais n 1 e   n 2 tais que I m   σ 1   e   I m   σ 2 estejam contidas em Ω. Suponha, ainda, que Γ1 é obtida de Γ2 poruma mudança de parâmetros que conserva a orientação (veja Seção 6.3).Prove

∫ ∫ σ 1   ∇ × F → ⋅   n → 1   d S = ∫ ∫ σ 2   ∇ × F → ⋅   n 2 →   d S

Interprete

Passo 1

Essa é uma questão puramente conceitual. O enunciado diz que “ Γ 1 é obtida de Γ 2 poruma mudança de parâmetros que conserva a orientação” ou seja Estamos falando de superfícies que tem a mesma fronteira. Como por exemplo a imagem abaixo

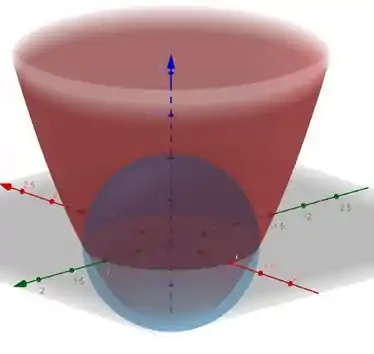
São duas superfícies, mas que compartilham a fronteira x 2 + y 2 = 1

Pelo teorema de stolkes

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   ∫ γ F ⋅ d r  

OU seja O fluxo através da superfície é igual ao trabalho feito pela nossa função percorrendo a fronteira. Se temos duas superfícies que tem a mesma fronteira, afinal :

Γ 1 =   Γ 2

O que implica em

∫ γ 1 F ⋅ d r = ∫ γ 2 F ⋅ d r

Por Stokes podemos dizer que

∫ ∫ σ 1   ∇ × F → ⋅   n → 1   d S = ∫ ∫ σ 2   ∇ × F → ⋅   n 2 →   d S

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S → . F → x , y , z = 2 yc o s zi → + e xs e n zj → + x e y k → , S é o hemisfério x 2 + y 2 + z 2 = 9 ,z ≥ 0 , orientado para cima.
Seja C uma curva fechada simples lisa que está no plano x + y + z = 1 . Mostre que a integral de linha ∫ C z d x - 2 x d y + 3 y d z depende apenas da área da região englobada por C e não da forma de
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = x i → + y j → + x y z k → , S é a parte do plano 2 x + y + z = 2 que está no primeiro octante, ori
Dado um hemisfério H e uma parte P de um paraboloide, suponha que F → seja um campo vetorial sobre R ³ ³cujas componentes tenham derivadas parciais contínuas. Explique por que ∬ H r o tF → ⋅d S → = ∬
Use o Teorema de Stokes para calcular ∫ C F → ⋅ d r → , onde F → x , y , z = x 2 z i → + x y 2 j → + z 2 k → e C é a curva da intersecção do plano x + y + z = 1 com o cilindro x 2 + y 2 = 9 com orient