Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 5

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva .

Onde é a fronteira do triângulo equilátero situado no plano de vértices , e

Passo 1

Falaa aíi jooveemm... Cadê a animação para mais uma questãozinha do Tio Stokes??

Booraaa...

Vamo ver quem diaxo é esse trianglin aí:

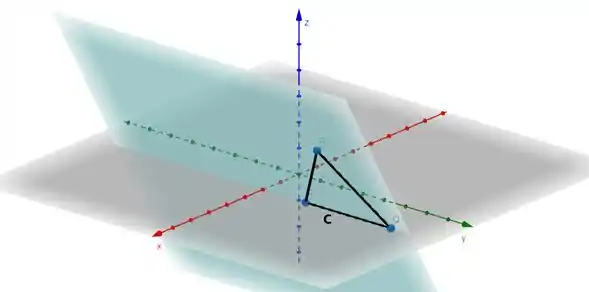
Taí o cujo dito. Portanto o enunciado nos diz que:

Mas sei lá em... não confio muito nesses caras. Vamos ver se isso é verdade mesmo??

Podemos utilizar o teorema de Stokes pra ver se é verdade mesmo ou não. O teorema diz o seguinte:

Onde é uma superfície cuja borda é a curva ... Canfundiu? Relaxa! Essa aqui é a nossa superfície:

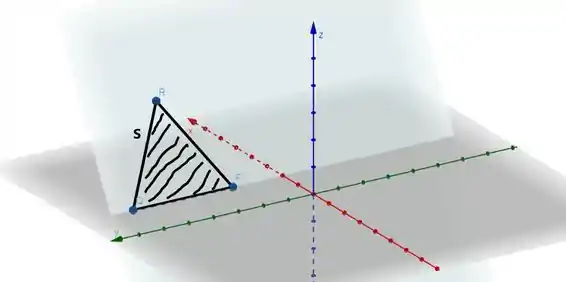
Percebe que a borda da superfície é a curva ?? Pouca diferença né? Mas é importante.

Então vamos obter os dados da integral dupla.

Passo 2

Começando pelo rotacional; você já deve (ou deveria) estar cansado de ver que o tal do rotacional é obtido assim:

Lembrando que:

Já sacou a ideia? É só encontrar essas derivadas parciais; olha só:

Então o nosso rotacional ficou assim:

Tranquilo demais. Agora precisamos de um tal que costumamos chamar de vetor normal.

Mas normal a quem?? A nossa superfície. Só que note que a nossa superfície esta contida num plano; então ser normal a superfície é também ser normal ao plano.

Se você se lembrar, dado um plano qualquer: o vetor normal à esse cara será: .

Então no nosso caso, seja o plano: ; teremos:

Show dibola. Então já podemos tacar na integral para ver o que se passa:

Passo 3

Isso vai ficar:

Aquela integral dupla de nada mais é do que a área do nosso brinquedo. Se a gente projetar a nossa superfície no plano vamos ter o seguinte:

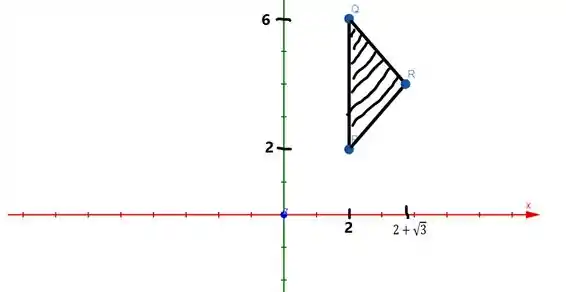
Onde e . Ou seja, a gente ignora a coordenada em pq estamos só no plano .

Então o que precisamos é da area desse triangulo aí. Lembra que para a area de um triangulo temos base vezes altura por doi?

Se a nossa base é e a nossa altura .

Então a area será:

That’s all!! See u!

Resposta

Concluindo, é verdade que:

Com a curva orientada no sentido anti-horário.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y 2 i → + x j → + z 2 k → , S é a parte do paraboloide z = x 2 + y 2 que está acima do plano z = 1

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = x + y 2 i → + y + z 2 j → + ( z + x 2 ) k → , C o triâ

Use o Teorema de Stokes para calcular ∫ C F → ⋅ d r → , onde F → x , y , z = x 2 y i → + x 3 3 j → + x y k → e C é a curva da intersecção do paraboloide hiperbólico z = y 2 - x 2 com o cilindro x 2 +

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k