Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 24
Seja e seja uma curva diferenciável cuja imagem está contida no gráfico de . Suponha, ainda, . Seja a reta tangente a em . Mostre que está contida no plano
Interprete geometricamente.
Passo 1
É dada uma função de duas variáveis e uma curva contida em , sendo que o único que conhecemos de é o seu valor em .
Este exercício é muito parecido com o anterior, com a diferença de que, agora, é desconhecida. Ela pode ser qualquer curva contida em !
Como não conhecemos a cara de , é bom já deixar a curva escrita através de sua componentes: .
Mas, como DEVE pertencer ao gráfico da (), deve existir a seguinte relação entre as componentes de :
Agora, vamos derivar a relação acima em relação a e deixar o resultado anotado:
Passo 2
Note que o ponto em refere-se a .
Agora, para determinar a reta tangente a no ponto , recorremos à figura abaixo:
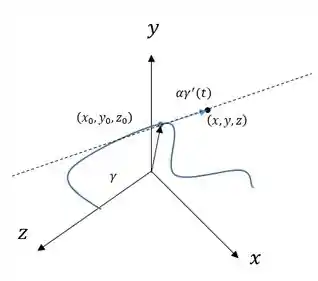
Note que, pela figura, um ponto qualquer sobre a reta tangente será dado pela soma do vetor ponto de referência, no caso , com o vetor , para algum número . Escrevendo isto em forma de equação, temos:
Mas, sendo , temos , ou, para , ficamos com:
Esta equação vetorial representa três equações:
Que é a equação da reta tangente no ponto!
Passo 3
Seja a reta obtida no item anterior. Devemos mostrar que esta reta satisfaz a equação:
Mas, nesta expressão,
E também
Assim, como , a equação que queremos testar fica
Agora, será que nossa reta se encaixa nesta equação? Bem, basta substituir o da reta ali para sabermos ao certo:
O que resulta em:
Será que esta equação é sempre satisfeita, independente da cara de ? Para responder isso, vamos invocar a equação que a gente deixou anotado logo no começo:
No ponto em que , temos e , e a relação acima fica:
As equações são idênticas! Isto significa que a única condição para estar contida no plano dado é ela existir!
A interpretação geométrica é simples: todas as retas tangentes a uma superfície num ponto estão no próprio plano tangente (o plano tangente é a coleção de todas as retas tangentes!).
Resposta
Ei, a resposta está no passo a passo :)