Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.4 - Ex. 9
Seja . Determine a reta tangente ao gráfico de , no ponto , que froma com o plano ângulo máximo.
Passo 1
Questãozinha de gradiente hein galera! (particularmente eu amo essas questões) Vamos dividir ela em passos e ir matando a questão de pouquinho hein poquinho, beleza?! SIMBORAAA! Primeiro, temos que saber do que se trata essa nossa função!!
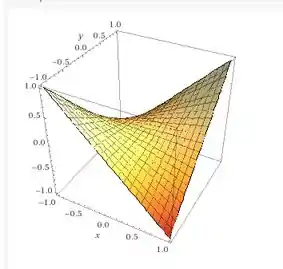
Essa é uma visualização 3D da função!! Para o gráfico em 2D de camadas, temos:
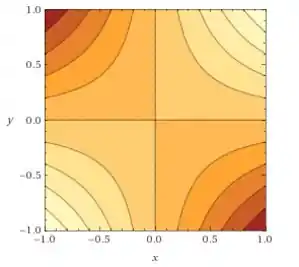
Passo 2
Vamos começar calculando
Como
Temos que
Então,
Passo 3
Sabemos que uma reta é composta por uma constante somada uma coisa que multiplica a variável que parametriza:
Para o nosso caso:
Quando temos
Então temos
E
Como
Passo 4
Então, nossa reta é
Substituindo pelo que a gente já achou nos passos anteriores, temos que:
Resposta
Exercícios de Livros Relacionados
Admita que T ( x , y )=16-2 x ²-y ² ² ² represente uma distribuição de temperatura no plano x y . Determine uma parametrização para a trajetória descrita por um ponto P que se desloca, a partir do pon
Seja f x , y = x y . Determine uma parametrização para a trajetória descrita por um ponto P que se desloca, a partir do ponto (1,2), sempre na direção e sentido de máximo crescimento de f .
Seja f x , y = x arctan x y . Calcule ∂ f ∂ u → ( 1,1 ) , onde u → aponta na direção e sentido de máximo crescimento de f , no ponto ( 1,1 ) .
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?a) f x , y = x 2 + x y + y 2 , em ( 1,1 ) .b) f x , y = ln x 2 + y