Seja
Esboce o gráfico e calcule o limite indicado se existir:
Passo 1
O gráfico da função é dado por:
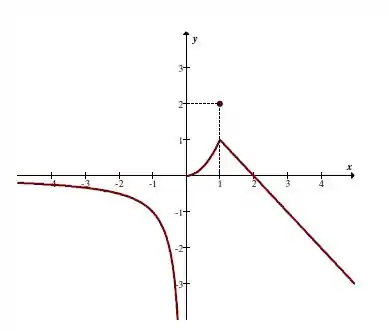
Passo 2
Para . Então, temos que:
Passo 3
Aplicando o limite, temos que:
Esse resultado pode ser concluído pensando que quando dividimos um número por outro muito pequeno o resultado da divisão tende a ser um número grande, por exemplo . Agora, pense que você está dividindo algo por um valor infinitesalmente pequeno, o resultado da divisão será infinitesalmente grande, logo infinito, e o sinal de mais se deve por estarmos analisando .