Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 4.10 - Ex. 54b

Seja f → a função vetorial definida por:

f → u ,   v = u . cos ⁡ v ,   u . s e n   v ,   3 + u 2

Para 0 ≤ u ≤ 3 ,   0 ≤ v ≤ 2 π .

b) Determinar ∂ f → ∂ u 3 , π 2 e ∂ f → ∂ v 3 , π 2 representando-os geometricamente.

Passo 1

Então galera, a função que nos foi dada é a seguinte:

f → u ,   v = u . cos ⁡ v ,   u . s e n   v ,   3 + u 2

Se derivarmos parcialmente, teremos:

∂ f → ∂ u = cos ⁡ v ,   s e n   v ,   2 u

∂ f → ∂ v = - u . s e n   v ,   u . cos ⁡ v ,   0

Passo 2

Tudo bem, agora que determinamos as derivadas, se substituirmos o ponto 3 , π 2 , teremos:

∂ f → ∂ u 3 , π 2 = cos ⁡   π 2 ,   s e n   π 2 ,   2 3

∂ f → ∂ u 3 , π 2 = 0 ,   1 ,   2 3

Para v , temos:

∂ f → ∂ v 3 , π 2 = - 3 . s e n   π 2 ,   3 . cos ⁡ π 2 ,   0

∂ f → ∂ v 3 , π 2 = - 3 ,   0 ,   0

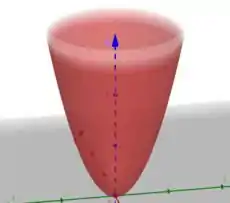
E essas são as derivadas parciais que procurávamos! Plotando, teremos:

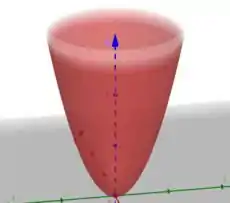
Vale ressaltar que é apenas um esboço do verdadeiro gráfico, tudo bem? Então é isso, galera! 😊

Resposta

∂ f → ∂ u 3 , π 2 = 0 ,   1 ,   2 3

∂ f → ∂ v 3 , π 2 = - 3 ,   0 ,   0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1. Determine as derivadas parciais c) z = x 3 + y 2 x 2 + y 2
1. Determine as derivadas parciais a) f x , y = 5 x 4 y 2 + x y 3 + 4
1. Determine as derivadas parciais g) f x , y = 4 x y - 3 y 3 3 + 5 x 2 y
2. Considere a função z = x y 2 x 2 + y 2 . Verifique que x ∂ z ∂ x + y ∂ z ∂ y = z .
1. Determine as derivadas parciais e) z = x 2 ln ⁡ 1 + x 2 + y 2