Seja . Mostre que é inversível e esboce os gráficos de e de sua inversa.
Passo 1
Oi, galerinha! Tudo bom? Antes de resolver esse exercício, note que temos e que é estritamente crescente, pois e são estritamente crescentes.
Se você der uma olhada no Exercício 12 vai ver que essas são as condições para que seja inversível.
Então agora só falta esboçar o gráfico!
Passo 2
Agora vamos esboçar os gráficos, com em verde e sua inversa em azul, que obtivemos refletindo o gráfico de em torno de (reta pontilhada):
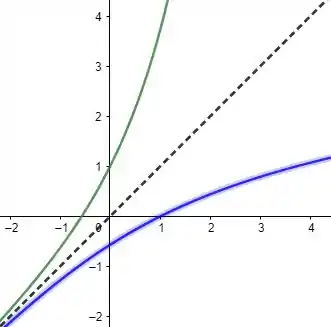
Resposta
Ei, a resposta está no passo a passo :)