Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.2 - Ex. 7
7 ) Seja , onde f (x, y z) = x + y + z. Desenhe F(x, y, z), com x+ y + z = 1, x > 0, y > 0 e z > 0
Passo 1
Para resolver essa questão temos que entender como é a interpretação de Gradiente. Quando definimos a reta normal de uma superfície qualquer – S
OU seja o vetor normal é o Gradiente com modulo 1. Assim eles tem o mesmo comportamento.
Passo 2
No nosso caso temos um plano , e o gradiente terá a mesma direção do vetor normal
E Gradiente tem o formato
Assim o gradiente do plano tem o seguinte vetor
Passo 3
Podemos observar esse vetor nas imagens abaixo
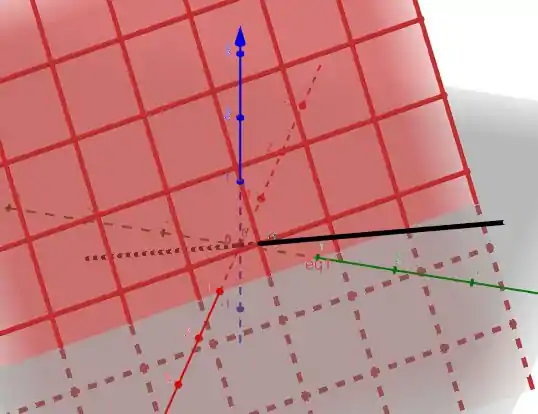
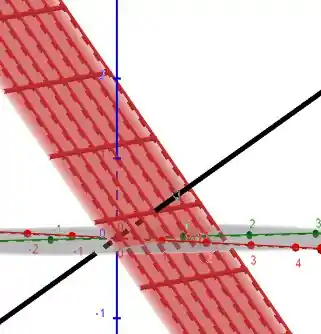
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine uma função f tal que F = ∇ f e Use a parte (a) para calcular ∫ F ⋅ d r sobre a curva C dada. F x , y , z = s e ny i ^ + x cos y + cos z j ^ - ( ys e nz ) k ^ C : r t = s e nti ^ + t j ^
Determine uma função f tal que F = ∇ f e Use a parte (a) para calcular ∫ F ⋅ d r sobre a curva C dada. F x , y , z = ( y 2 z + 2 x z 2 ) i ^ + ( 2 x y z ) j ^ + ( x y 2 + 2 x 2 z ) k ^ C : x = t ,y =
Determine uma função f tal que F = ∇ f e Use a parte (a) para calcular ∫ F ⋅ d r sobre a curva C dada. F x , y , z = y z i ^ + x z j ^ + ( x y + 2 z ) k ^ C é a o segmento de linha de ( 1,0 , - 2 ) pa
Determine uma função f tal que F = ∇ f e Use a parte (a) para calcular ∫ F ⋅ d r sobre a curva C dada. F x , y , z = ( y 2 z + 2 x z 2 ) i ^ + ( 2 x y z ) j ^ + ( x y 2 + 2 x 2 z ) k ^ C : x = t ,y =
Determine se F é um campo vetorial conservativo ou não. Se for, encontre a função f tal que F = ∇ f . F x y = 2 x y + y - 2 i ^ + x 2 - 2 x y - 3 j ^ , y0