Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 101e
Seja
(e) O resultado da parte (d) contradiz o Teorema de Clairaut? Use os gráficos de e para ilustrar sua resposta.
Passo 1
E aí, galera. Tudo bem? Nessa questão nós queremos saber se a função contradiz o Teorema de Clairaut.
Para responder isso, nós precisamos lembrar o que é esse teorema e aplicar isso ao caso da função dada.
Depois, vamos plotar os gráficos de e para analisar se o que fizemos está coerente.
Tranquilo? Então vamos lá...
Passo 2
O teorema de Clairaut nos diz o seguinte: Suponha que seja definida em uma bola aberta que contenha o ponto . Se as funções e são continua em D, então:
No item anterior, vimos que e . Como as derivadas não são iguais em , ficamos tentados em dizer que a função não atende ao Teorema de Clairaut.
Entretanto, as funções e não são contínuas em Assim, a função não contradiz o teorema de Clairaut.
Passo 3
Vamos usar os gráficos de e para entender a nossa resposta:
– Gráfico de
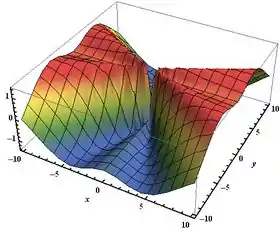
– Gráfico de
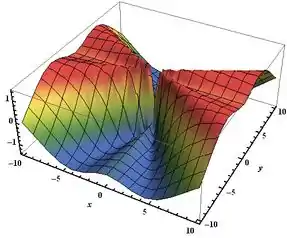
Como podemos perceber nos gráficos, há uma descontinuidade em , de modo que não podemos aplicar o Teorema de Clairaut.
Resposta
Não contradiz, uma vez que as funções e não são contínuas em