Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.8 - Ex. 12
Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
Show de bola, galera! Precisamos esboçar o sólido descrito pelas seguintes desigualdades:
Precisamos encontrar uma forma de escrever as coordenadas e e mfunção dessas desigualdades, e encontrar quais pontos farão parte desse sólido para criar o traçado. Para isso, iremos utilizar as relações de coordendas cilíndricas para cartesianas.
Vamos ver como será feito?
Passo 2
Partiu plotar o gráfico dessa região . Só não podemos nos esquecer de que:
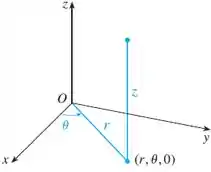
Onde:
Então:
Veja que se é do tipo:
Então a base de tem uma aparência circular que aumenta linearmente com o raio , limitada em
Podemos traçar uma linha de . E depois saberemos que temos o cone com raio igual à linha traçada. Mas como máximo é estamos limitados a oprimeiro octante. Veja:
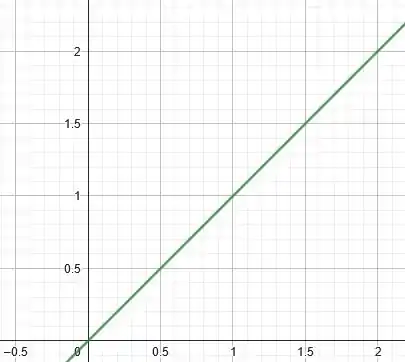
Agora imagine uma revolução em torno de , mas apenas de volta.
Partiu... Cone no primeiro quadrante:
Resposta
Gráfico desenhado