Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 10

Seja o tetraedro de vértice ; ; e . Sejam a superfície lateral de constituída pelas faces de que não estão no plano , e , um campo vetorial de . Calcule , com a normal exterior a .

Passo 1

Faaalaaa joveeem... Partiu mais uma questãozinha?? Let’s bora!

Sempre lembrando que essa matéria exige que tu sejas não só bom em cálculo, mas também um exímio desenhista. A gente tem que buscar essa superfície:

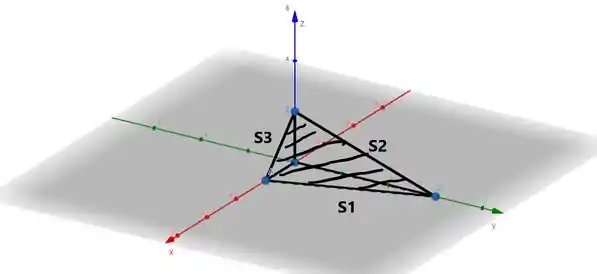
A superfície é a “união” de todas essas três superfícies que não estão no plano.

Então podemos escrever o seguinte:

Se você bem lembra, para podermos aplicar o teorema de Gauss é condição necessária que a curva seja FECHADA.

Então não poderíamos aplicar isso aqui porque a superfície não leva em consideração a base.

Mas como a gente é do contra, vamos colocar o diaxo da base sim!

Então repare que:

Pegou a ideia??

Ou seja, o que a gente tá procurando é:

Vamos correr atrás disso daê!

Passo 2

Começando com a integral tripla que é na verdade a aplicação do teorema de Gauss.

Começando pelo divergente; lembrando que a gente acha ele assim:

Onde:

Chegaremos em:

Ouu seeejaaa:

Simples assim BB.

Passo 3

Próxima!

Aqui se trata quase que de teorema de Stokes; ta lembrado?

Vamos atrás desse rotacional (só falta ser zero também)...

Só precisamos desses diferenciais:

Portanto o nosso rotacional:

Antes de tacarmos tudo na integral, falta o vetor normal. Não tem muito segredo o vetor está normal ao plano .

Achar um vetor normal a qualquer plano é bem tranquilo, olha só.

Seja o plano o vetor normal será: .

Então como a base ta no plano , que pode na verdade ser escrito como: ; o nosso vetor será:

Por que?? Porque o enunciado diz que o vetor normal é exterior, então ele tem que estar “apontado” pra baixo. Pegou a ideia??

Agora podemos tacar na integral:

Perceba que:

Ou seja, precisamos da área daquele trianglin da base ali.

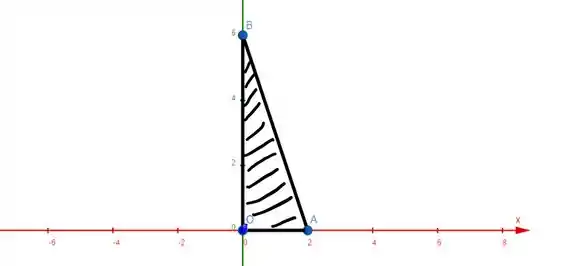
Como que a gente acha a área mesmo?? Base vezes altura por dois; lembra?

Portanto:

Maaasss caarmeeeiaaa que ainda não é a resposta!

Lembra que a gente definiu:

Então:

That’s! See u...

Resposta

Concluimos que:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F → x , y , z = x y 2 i → + x y zj → + z - y 2 z - 1 2 x z 2 k → e seja σ a superfície x 2 + y 2 + z 2 = 1 , z ≥ 0 , sendo n → a normal com componente z ≥ 0 . Calcule ∬ σ F → ⋅ n →d S .

Seja u → um campo vetorial de classe C 2 num aberto Ω ⊂ R 3 e seja B ⊂ Ω um compacto ao qual o teorema da divergência se aplica. Seja σ a fronteira de B , com normal n → apontando para fora de B . Cal

Calcule ∬ σ u → ⋅ n →d S sendo σ a fronteira de B com normal exterior n → sendo: d )B = x , y , z ∈ R 3 x 2 + y 2 ≤ 1 ,x 2 + y 2 ≤ z ≤ 5 - x 2 - y 2 } e u → = 3 x y i → - 3 2 y 2 j → + z k → .

11. Sejam f, g : Ω ⊂ ℝ3 → ℝ de classe C2 no aberto Ω. Seja B ⊂ Ω uma esfera e seja σ a fronteira de B, com normal exterior . Proveb. ∫ ∫ σ f ∂ g ∂ n d S = ∫ ∫ ∫ B f ∇ 2 g + ∇ f ⋅ ∇ gd V

12 . a . Sejam u e v dois campos vetoriais de classe C1 em ℝ 3 ; seja B uma esfera com fronteira σ e normal exterior . Suponha que r o tu =r o tved i vu =d i vv . Suponha, ainda, que u · v=v · u sobre