Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 8

Seja A = { x ,   y ∈ R 2 | 0 < x 2 + y 2 + 2 y + 1 < 1 } . Verificar se os pontos:

a )   0 ,   - 1 2

b )   ( 0 ,   - 1 )

c )   ( - 1 ,   - 1 )

d )   ( 1 ,   1 )

e )   ( 0 ,   0 )

f ( 3 ,   4 )

são pontos de acumulação de A .

Passo 1

Pra começar a gente tem que saber que figura é essa que o conjunto A representa, né? Bom, a gente já tá craque em reconhecer essas paradas, e você já tá vendo que isso tem a maior cara de circunferência. Realmente, se a gente mexer um pouco, vamos ver:

x 2 + y 2 + 2 y + 1 < 1

Elevando ao quadrado:

x 2 + y 2 + 2 y + 1 < 1

Agrupando,

x 2 + y + 1 2 < 1

Isso representa uma bola aberta, de raio 1 e centro ( 0 ,   - 1 ) .

No plano cartesiano, a figura tem essa cara aqui:

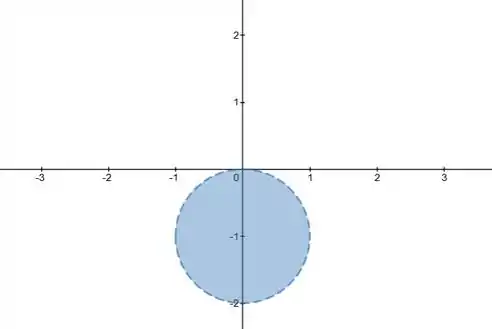
Passo 2

E agora, pra decidir quais pontos são pontos de acumulação? Bom, não tem mistério! É só a gente marcar os pontos na figura, e ver quais estão dentro da região (ou na bordinha), o que significa que os pontos atendem à equação que define o conjunto!

Vamos marcar todos os pontos.

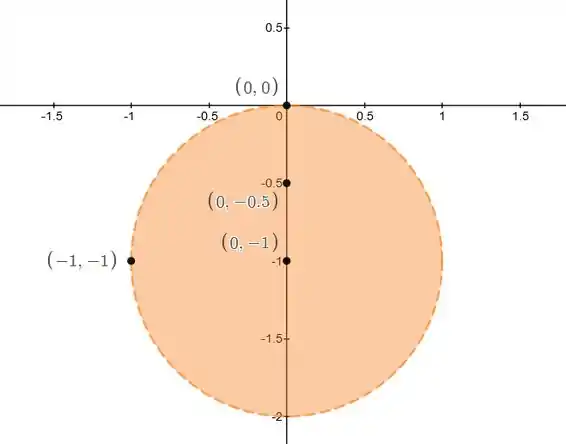
Os pontos que nos interessam, ou seja, os pontos de acumulação, foram esses que ficaram na região da circunferência, e os outros não são. Ou seja:

A , B , C e E são pontos de acumulação e D e F não são.

Resposta

A , B , C e E são pontos de acumulação e D e F não são.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontrar a curva de interseção do gráfico da função dada com os planos dados, representando graficamente:(b) z = x 2 + y 2 com os planos z = 1 ; x = 0 ; y = x .
Encontrar a curva de interseção do gráfico da função dada com os planos dados, representando graficamente:(c) z = 4 - x 2 - y 2 com os planos z = 1 ; x = y ; y = 0 .
Fazer um esboço de algumas superfícies de nível da função w = x 2 + y 2 + z 2 . O que ocorre com os valores da função ao longo de semi-retas que partem da origem?
Sabendo que a função T x , y , z = 30 - x 2 + 1 4 y 2 + 1 9 z 2 representa a temperatura nos pontos da região do espaço delimitada pelo elipsoide x 2 + y 2 4 + z 2 9 = 1 pergunta-se:Em que ponto a tem
Esboçar o gráfico das superfícies de nível S k correspondentes aos valores de k dados:(b) w = x 2 + y 2 ; k = 4 ,16 ,25