Enunciado
Álgebra Linear e Geometria Analítica - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.3 - Ex. 15
Sejam dados e com . Verifique que é a equação vetorial do plano que passa por e que é perpendicular a .
Passo 1
O enunciado nos pede para encontrarmos o plano que passa pelo ponto e é perpendicular a , e a seguir comparar com a equação dada.
Os dados que o problema fornece são:
-Os vetores e ;
-O ponto , que pertence ao plano e é conhecido; e
-O ponto , que também pertence ao plano, mas deve ser determinado por nós em função dos 2 dados acima.
O enunciado também dos informa que . Trata-se de apenas um formalismo para dizer que e não são colineares e portanto existe um plano formado por e . Este dado não interfere nos cálculos.
Passo 2
Para matar a questão a pau, basta desenharmos os dados do problema:
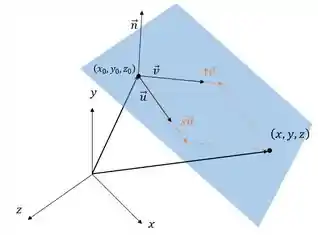
Só de olhar para a figura, podemos afirmar que qualquer ponto do plano pode ser construído a partir do ponto inicial e mais “alguma combinação” dos vetores e . Vamos designar esta combinação por , onde e são números. Assim, a nossa afirmação, equacionada, daria o seguinte:
Que é o que precisávamos verificar!
Resposta
Ei, a resposta está no passo a passo :)