Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.6 - Ex. 21

Sejam P = 0 , a e Q = b , c , onde a , b e c são números reais dados e estritamente positivos. Seja M = x , 0 , com 0 ≤ x ≤ b .

  1. Determine x para que o perímetro do triângulo P M Q seja mínimo.
  2. Conclua que o perímetro será mínimo para α = β .

Passo 1

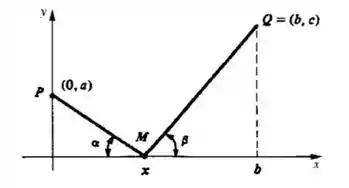
Vamos primeiro definir a equação para o perímetro do triângulo P M Q :

2 P = M Q - + P Q - + M P -

O lado M Q - é a hipotenusa do triângulo M N Q , onde N = b , 0 .

M Q - 2 = c 2 + b - x 2

M Q - = c 2 + b - x 2

Já o lado M P - é a hipotenusa do triângulo M O P , onde O = 0,0 .

M P - 2 = x 2 + a 2

M P - = x 2 + a 2

Por fim, o lado P Q - é a hipotenusa do triângulo P Q Z , onde Z = 0 , c .

P Q - 2 = c - a 2 + b 2

P Q - = c - a 2 + b 2

Para o perímetro ser mínimo, d 2 P / d x = 0 .

d 2 P d x = c 2 + b - x 2 + x 2 + a 2 + c - a 2 + b 2 ' = 0

1 2 ∙ 1 c 2 + b - x 2 c 2 + b - x 2 ' + 1 2 ∙ 1 x 2 + a 2 x 2 + a 2 ' + 0 = 0

1 c 2 + b - x 2 0 - 2 b + 2 x + 1 x 2 + a 2 2 x + 0 = 0

- 2 b + 2 x c 2 + b - x 2 + 2 x x 2 + a 2 = 0

- b + x c 2 + b - x 2 = - x x 2 + a 2

Vamos elevar os dois lados ao quadrado:

- b + x c 2 + b 2 - 2 b x + x 2 2 = - x x 2 + a 2 2

x 2 - 2 b x + b 2 c 2 + b 2 - 2 b x + x 2 = x 2 x 2 + a 2

x 4 - 2 b x 3 + b 2 x 2 + a 2 x 2 - 2 a 2 b x + a 2 b 2 = c 2 x 2 + b 2 x 2 - 2 b x 3 + x 4

a 2 x 2 - 2 a 2 b x + a 2 b 2 = c 2 x 2

a 2 - c 2 x 2 + - 2 a 2 b x + a 2 b 2 = 0

Aplicando Bhaskara:

x = 2 a 2 b ± - 2 a 2 b 2 - 4 a 2 - c 2 a 2 b 2 2 a 2 - c 2

x = 2 a 2 b ± 4 a 2 b 2 c 2 2 a 2 - c 2 = 2 a 2 b ± 2 a b c 2 a 2 - c 2 = a b a ± c a + c a - c

x 1 = a b a + c

x 2 = a b a - c

Como c > a , temos x = a b a + c .

Passo 2

Na letra a.) encontramos o valor de x para o perímetro mínimo. O exercício pede para provarmos que α = β no perímetro mínimo, para isso:

tan ⁡ α = a x

tan ⁡ β = c b - x

Se α = β :

tan ⁡ α = tan ⁡ β

a x = c b - x

a b - a x = c x

c x + a x = a b

x a + c = a b → x = a b a + c

Resposta

  1. x = a b a + c
  2. Sim
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os números críticos da função. g t = t 4 + t 3 + t 2 + 1
Encontre os números críticos da função. g y = y - 1 y 2 - y + 1
Encontre os valores máximo e mínimo absolutos de f no intervalo dado. f x = 3 x 4 - 4 x 3 - 12 x 2 + 1 , [ - 2,3 ]
Encontre os valores máximo e mínimo absolutos de f no intervalo dado. f x = x + 1 x , [ 0,2 ; 4 ]
Encontre os valores máximo e mínimo absolutos de f no intervalo dado. f x = x - 2t g - 1 x ,[ 0,4 ]