Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.4 - Ex. 9

9. y = 1 - ln (sen x) , (pi)/(6) <= x <= (pi)/(4)

Passo 1

Nós devemos encontrar o comprimento da curva dada.

 Nós temos:

y = 1 - ln (sen x)

(d y)/(d x) = - (c o s x)/(s e n x)

Passo 2

Agora prosseguimos da seguinte maneira:

1 + ((d x)/(d y))^2 = 1 + (- (c o s x)/(s e n x))^2

= 1 + (cos^2 x)/(sen^2 x)

Passo 3

Agora, pela fórmula do comprimento da curva, temos:

s = int_((pi)/(6))^((pi)/(4)) sqrt(1 + (cos^2 x)/(sen^2 x)) d x

= int_((pi)/(6))^((pi)/(4)) sqrt((sen^2 x + cos^2 x)/(sen^2 x)) d x

Por definição sen^2 x + cos^2 x = 1

= int_((pi)/(6))^((pi)/(4)) (d x)/(sen x)

= int_((pi)/(6))^((pi)/(4)) c o s c x d x

No final do livro, temos a Tabela de Integrais, onde conseguimos a resposta para a integral acima.

= (ln | c o s e c x - cotg x ||_((pi)/(6))^((pi)/(4))

= ln |(2)/(sqrt(2)) - 1| - ln |2 - (sqrt(3))/(sqrt(3))|

= ln |(2 - sqrt(2))/(sqrt(2)) * ((sqrt(3))/(2 sqrt(3) - 1))|

= ln |(2 sqrt(3) - sqrt(6))/(2 sqrt(6) - sqrt(2))|

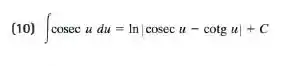
Resposta

Portanto, o comprimento da curva é  ln |(2 sqrt(3) - sqrt(6))/(2 sqrt(6) - sqrt(2))|

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a fórmula do comprimento de arco do Exercício 26 para encontrar o comprimento de arco da curva. x = 1 3 t 3 ,y = 1 2 t 2 0 ≤ t ≤ 1
O segmento curvilíneo y = x 2 de x = 1 até x = 2 pode também ser expresso como o gráfico de x = y de y = 1 até y = 4 . Monte duas integrais que deem o comprimento de arco desse segmento, uma usando in
Use a fórmula do comprimento de arco do Exercício 26 para encontrar o comprimento de arco da curva. x = cos ⁡ 2 t ,y = s e n2 t , ( 0 ≤ t ≤ π 2 )
Considere os segmentos de curva y = x 2 de x = 1 2 até x = 2 e o segmento de curva y = x de até x = 1 4ex = 4 . (a) Faça o gráfico dos dois segmentos de curva e utilize-os para explicar por que os com
Use a fórmula do comprimento de arco do Exercício 26 para encontrar o comprimento de arco da curva. x = e t cos ⁡ t ,y = e t s e nt , ( 0 ≤ t ≤ π 2 )