Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.1 - Ex. 7
Sistemas de equação de primeira ordem podem ser transformados, algumas vezes, em uma única equação de ordem maior. Considere o sistema:
(a) Resolva a primeira equação para e substitua na segunda equação, obtendo, assim, uma equação de segunda ordem para . Resolva essa equação para e depois determine também .
(b) Encontre a solução do sistema dado que também satisfaz as condições iniciais , .
(c) Esboce a curva, para , dada em forma paramétrica pelas expressões para e encontradas em (b).
Passo 1
O item (a) nos pede para resolver o sistema de equações. Para isso, vamos primeiro deixar em função de :
Substituindo na segunda equação:
Se ,
Então, nossa equação fica:
Então a solução para é:
Em que e são duas constantes quaisquer.
Agora que encontramos podemos usá-lo para obter :
Passo 2
Vamos agora para o item (b). Ele nos pede para encontrar as funções e que também atendem aos valores de condição inicial , .
Como vimos no item (a) a função que é solução do problema é:
Para :
Analogamente, encontramos a solução para :
Para :
Ficamos então com o seguinte sistema:
Então:
Substituindo as cosntantes e nas funções solução:
Passo 3
Nosso último passo é desenhar as curvas e que encontramos no item (b). Elas são esboçadas a seguir:
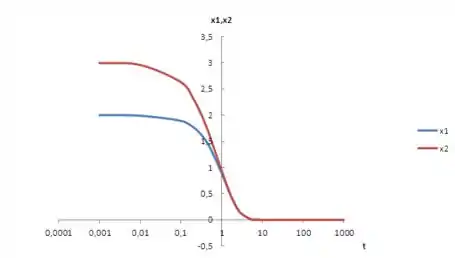
Resposta
Ei, a resposta está no passo a passo :)