Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 50

Se E o é o sólido do Exercício 18 com função densidade ρ x , y , z = x 2 + y 2 , determine as seguintes quantidades, com precisão de três casas decimais.

  1. A massa
  2. O centro de massa
  3. O momento de inércia em relação ao eixo z

Passo 1

Faala, tudo certo?

Nessa questão precisamos calcular três coisas: massa, centro de massa, e momento de inércia em relação ao eixo z .

Nós temos o sólido E , e a função densidade ρ x , y , z = x 2 + y 2 .

Com isso, temos as fórmulas da massa:

m = ∭ E ρ x , y , z d V

Do centro de massa x - , y - , z - :

x - = 1 m ∭ E x ∙ ρ x , y , z d V

y - = 1 m ∭ E y ∙ ρ x , y , z d V

z - = 1 m ∭ E z ∙ ρ x , y , z d V

E do momento de inércia em relação ao eixo z :

I z = ∭ E x 2 + y 2 ∙ ρ x , y , z d V

O sólido E foi estudado no exercício 18 , onde encontramos os limites das variáveis:

0 ≤ z ≤ 9 - y 2

3 x ≤ y ≤ 3

0 ≤ x ≤ 1

Então vamos usar isso pra transformar essas integrais em integrais iteradas e calcular!

Essa questão é marcada como SCA – ou seja, precisamos usar um sistema de computação algébrica pra calcular as integrais. Eu vou usar o WolframAlpha!

Passo 2

(a)

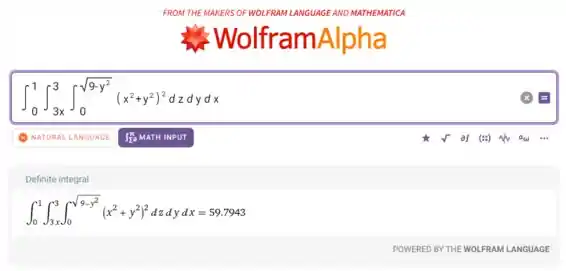
A massa é dada por

m = ∭ E x 2 + y 2 d V

Aplicando os limites do sólido ficamos como:

m = ∫ 0 1 ∫ 3 x 3 ∫ 0 9 - y 2 ( x 2 + y 2 )   d z d y d x

Vamos usar o WolframAlpha pra achar o valor dessa integral:

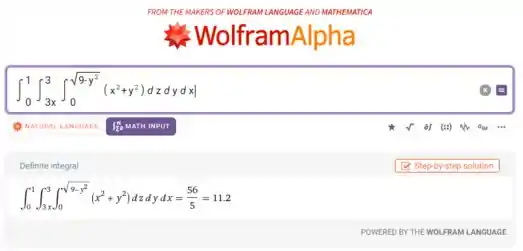
Então,

m = 56 5 = 11,2

Passo 3

(b)

O centro de massa é ( x - , y - , z - ) .

Para a coordenada x :

x - = 1 m ∭ E x x 2 + y 2 d V

= 5 56 ∫ 0 1 ∫ 3 x 3 ∫ 0 9 - y 2 x ( x 2 + y 2 )   d z d y d x

Calculando (como 5 / 56 é constante, ele pode ser colocado pra dentro da integral, e vamos fazer assim pra facilitar o input):

x - ≈ 0,375

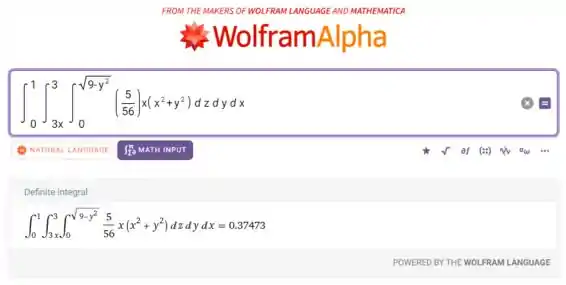
Para y - :

y - = 1 m ∭ E y x 2 + y 2 d V

= 5 56 ∫ 0 1 ∫ 3 x 3 ∫ 0 9 - y 2 y ( x 2 + y 2 )   d z d y d x

No software:

y - = 45 π 64 ≈ 2,209

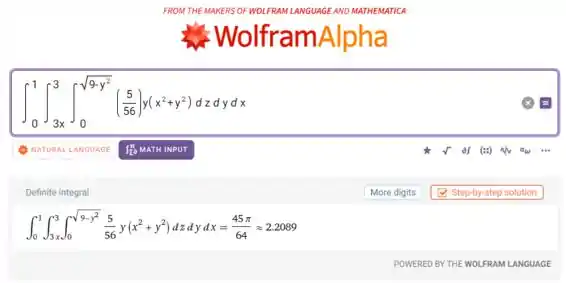
Por último, para z :

z - = 1 m ∭ E z x 2 + y 2 d V =

= 1 m ∫ 0 1 ∫ 3 x 3 ∫ 0 9 - y 2 z ( x 2 + y 2 )   d z d y d x

No WolframAlpha:

z - = 15 16 = 0,9375

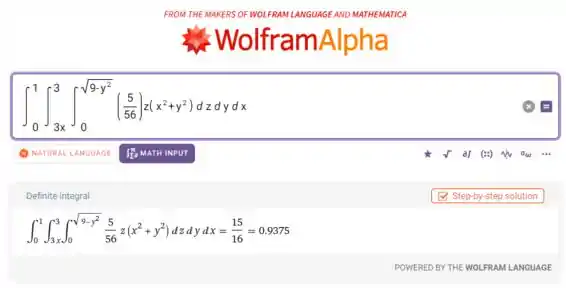
Então o centro de massa (com três casas decimais) fica:

x - , y - , z - = 0.375,2.209,0.938

Passo 4

(c)

Finalmente, o momento de inércia em relação ao eixo z é dado por

I z = ∭ E x 2 + y 2 x 2 + y 2   d V

= ∫ 0 1 ∫ 3 x 3 ∫ 0 9 - y 2 x 2 + y 2 2   d z d y d x

Calculando:

I z ≈ 59,794

Resposta

  1. m = 11,200

  2. 0.375 ,   2.209 ,   0.938

I z ≈ 59,794

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o momento de inércia do corpo homogêneo x + y + z ≤ 4 , x ≥ 0 , y ≥ 0 e z ≥ 0 , em relação ao eixo z .
Calcule o momento de inércia de um cone circular reto de altura h , raio da base R , homogêneo, em relação a um diâmetro de sua base.
Considere um cone circular reto homogêneo de altura h e raio de base R .Calcule o centro de massa.Calcule o momento de inércia em relação ao seu eixo.
Aplique o Teorema de Steiner ao item b do Exercício 4.
Calcule o cilindro homogêneo x - a 2 + y 2 ≤ a 2 e 0 ≤ z ≤ h Calcule o momento de inércia em relação à reta x = a e y = 0 Calcule o momento de inércia em relação ao eixo O z .