Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.4 - Ex. 5
Suponha contínua em e periódica com período em , isto é, para todo .
Prove que a função
é constante. Interprete graficamente.
Passo 1
O teorema fundamental do cálculo nos dá,
Passo 2
Aplicando ao problema,
Sabendo que é uma função periódica,
Qual a única maneira de a derivada de ser
Passo 3
Interpretando graficamente (usando uma função periódica qualquer),
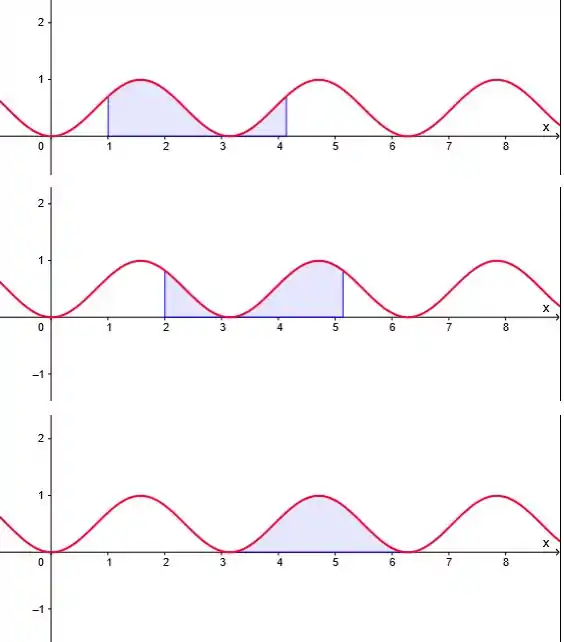
Constata-se que a área de um intervalo do tamanho do período, for igual
Resposta
Pelo teorema fundamental do cálculo, conclui-se que se for uma função periódica, será uma constante.
Exercícios de Livros Relacionados
Ache a derivada da função g x = ∫ tan x x 2 1 2 + t 4 d t
Se f 1 = 12 , f ' é contínua e ∫ 1 4 f ' x d x = 17 , qual é o valor de f ( 4 ) ?
Ache a derivada da função y = ∫ cos x 5 x c o s ( u 2 ) d u
Ache o intervalo em que a curva y = ∫ 0 x 1 1 + t + t 2d t É côncava para cima.
Se F x = ∫ 1 x f t d t Onde f t = ∫ 1 t 2 1 + u 4 ud u Determine F ' ' ( 2 )