Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.4 - Ex. 14

A tabela fornece a população da Espanha em meados do ano, em milhares, de a

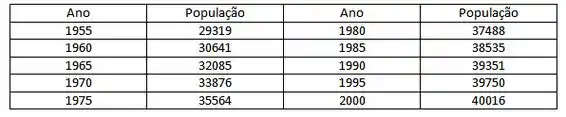
Use uma calculadora gráfica para ajustar tanto uma função exponencial quanto uma função logística a estes dados. Marque os pontos, trace ambas as funções e comente a precisão dos modelos. [Sugestão: Subtraia de cada valor da população. Então, depois de obter um modelo de sua calculadora, some para obter seu modelo final. Pode ser útil escolher como ou

Passo 1

Galera, aqui vamos ter que usar uma calculadora gráfica pra achar qual a melhor função exponencial e qual a melhor função logística que mais se ajustam aos pontos fornecidos pela tabela.

Seguindo a sugestão que o enunciado nos deu, nós escolhemos para corresponder a e subtraímos de cada valor da população. Então usamos uma calculadora para obter os modelos exponencial e logístico e adicionamos de volta, pra no final chegarmos a:

sendo e as populações fornecidas pelos modelos exponencial e logístico, respectivamente.

Passo 2

Agora vamos desenhar os gráficos das duas funções que obtemos, junto com os pontos da tabela, pra fazer uma comparação:

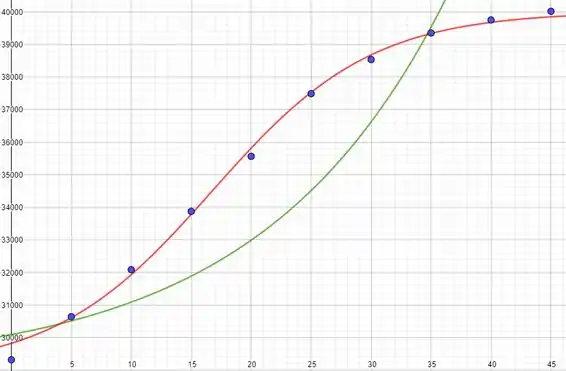
Em vermelho, a função logística; em verde, a função exponencial

Parece que o modelo logístico é bem mais razoável, né? Ele conseguiu ser bastante fiel aos dados da tabela, enquanto o modelo exponencial só é uma boa aproximação para os pontos iniciais. Beleza?

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reações químicas de primeira ordem Em algumas reações químicas, a taxa à qual a quantidade de uma substância varia em relação ao tempo é proporcional à quantidade presente. Para a transformação da glu

Trabalho sob a água. A intensidade L ( x ) de luz x pés sob a superfície do oceano satisfaz a equação diferencial d L d x = - k L Como mergulhador, você sabe, por experiência, que um mergulho de 18 pé

Pressão atmosférica. A pressão atmosférica p da Terra frequentemente é modelada pela suposição de que a taxa d p / d h à qual p varia com a altitude h acima do nível do mar é proporcional a p . Suponh

Esgotamento de petróleo. Suponha que a quantidade de petróleo bombeada de um dos poços do canyon em Whittier, na Califórnia, tenha diminuído a uma taxa contínua de 10 % ao ano.Quando a produção do poç

Esfriamento de sopa. Suponha que, após 10 minutos em uma sala cuja temperatura seja 20 ° C , a temperatura de uma tigela com sopa tenha passado de 90 ° C para 60 ° C . Use a lei do resfriamento de New