Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 50

Temperatura em uma elipse. Seja T = g x ,   y a temperatura no ponto x ,   y na elipse

e suponha que

a. Localize as temperaturas máxima e mínima na elipse examinando d T / d t e d 2 T / d t 2 .

b. Suponha que T = x y - 2 . Encontre os valores máximo e mínimo de T na elipse.

Passo 1

Oi pessoal, tudo bem com vocês? Vamos lá! Primeiramente a gente vai desenhar o diagrama de árvore:

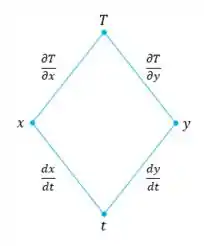
Com o diagrama, conseguimos definir a Regra da Cadeia:

d T d t = ∂ T ∂ x d x d t + ∂ T ∂ y d y d t

Passo 2

Com x = 2 2 cos ⁡ t y = 2 sen ⁡ t     conseguimos transformar as derivadas em função de t :

∂ T ∂ x = y = 2 sen ⁡ t

∂ T ∂ y = x = 2 2 cos ⁡ t

Substituindo na equação da Regra da Cadeia:

d T d t = 2 sen ⁡ t ∙ - 2 2 sen ⁡ t + 2 2 cos ⁡ t ∙ 2 cos ⁡ t

= - 2 ∙ 2 ∙ sen 2 ⁡ t + 2 ∙ 2 ∙ cos 2 ⁡ t

= 4 cos 2 ⁡ t - sen 2 ⁡ t

Sabemos que cos 2 ⁡ t - sen 2 ⁡ t = cos ⁡ 2 t , logo:

d T d t = 4 cos ⁡ 2 t

Agora iremos calcular d 2 T / d t 2 :

d 2 T d t 2 = ∂ 2 T ∂ x 2 d 2 x d t 2 + ∂ 2 T ∂ y 2 d 2 y d t 2

= 0 ∙ - 2 2 cos ⁡ t + 0 ∙ - 2 sen ⁡ t

Então temos a nossa segunda derivada:

d 2 T d t 2 = 0

Passo 3

Igualando a primeira derivada a zero:

cos ⁡ 2 t = 0

2 t = cos - 1 ⁡ 0

Temos 2 opções:

2 t = π 2 2 t = 3 π 2

Logo:

t = π 4 t = 3 π 4

Mas como sabemos pelas propriedades das funções trigonométricas que cos ⁡ θ = cos ⁡ - θ , então temos 4 valores para t : - π / 4 , π / 4 , - 3 π / 4 e 3 π / 4 .

Passo 4

Para os 4 valores que encontramos para t , iremos encontrar seus respectivos valores de x e y :

t = - π 4 → x = 2       y = - 1

t = π 4 → x = 2 y = 1

t = - 3 π 4 → x = - 2 y = - 1

t = 3 π 4 → x = - 2 y = 1      

Onde os pontos 2 ,   1 e - 2 ,   - 1 são máximos e os pontos 2 ,   - 1 e - 2 ,   1 são mínimos

Passo 5

No item b., temos a seguinte equação:

T = x y - 2

Para os pontos máximos, temos:

T m a x = 2 ∙ 1 - 2 = 0

T m a x = - 2 ∙ - 1 - 2 = 0

E para os pontos mínimos:

T m i n = 2 ∙ - 1 - 2 = - 4

T m i n = - 2 ∙ 1 - 2 = - 4

Resposta

  1. Máximo 2 ,   1 e - 2 ,   - 1 ;

    2. Mínimo 2 ,   - 1 e - 2 ,   1 .

  2. T m a x = 0 ;

T m i n = - 4 .

Exercícios de Livros Relacionados

Nos Exercícios 9 e 10, (a) expresse ∂ w / ∂ u e ∂ w / ∂ v como funções de u e v utilizando a regra da cadeia e também expressando w diretamente em termos de u e v antes de diferenciar. Em seguida, (b)
Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada. ∂ w ∂ s para w = g x ,y , x = h r ,s ,t , y = k r ,s ,t
Variações de voltagem em um circuito. A voltagem V em um circuito que satisfaz a lei V = I R vai caindo lentamente à medida que a bateria descarrega. Ao mesmo tempo, a resistência R vai aumentando con
Coordenadas polares. Suponha que substituamos as coordenadas polares x = r cos ⁡ θ e y = r sen ⁡ θ em uma função derivável w = f x ,y .a. Mostre que ∂ w ∂ r = f x cos ⁡ θ + f y sen ⁡ θ e 1 r ∂ w ∂ θ =
Se f (u , v , w) é diferenciável e u = x - y , v = y - z e w = z - x , mostre que(del f)/(del x) + (del f)/(del y) + (del f)/(del z) = 0