Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 30

Traçar as curvas de nível de f x , y = 1 2 x 2 + 1 2 y 2 que passem pelos pontos 1,1 , 1 , - 2 e - 2 , - 1 . Traçar os vetores ∇ f 1,1 , ∇ f 1 , - 2   e   ∇ f - 2 , - 1 .

Passo 1

Para acharmos as curvas de níveis, basta verificarmos o valor de f x , y no ponto x 0 ,   y 0 . Em seguida, representamos o plano z = f x 0 , y 0 .

f x , y = 1 2 x 2 + 1 2 y 2

Passo 2

Então vamos lá! Para o ponto 1,1 :

f 1,1 = 1 2 × 1 2 + 1 2 × 1 2

Logo,

f 1,1 = 1

Para o ponto 1 , - 2 :

f 1 , - 2 = 1 2 × 1 2 + 1 2 × - 2 2

Portanto,

f 1 , - 2 = 5 2

Por fim, vamos verificar para o ponto - 2 , - 1 :

f - 2 , - 1 = 1 2 × - 1 2 + 1 2 × - 2 2

Fazendo as contas:

f - 2 , - 1 = 5 2

Passo 3

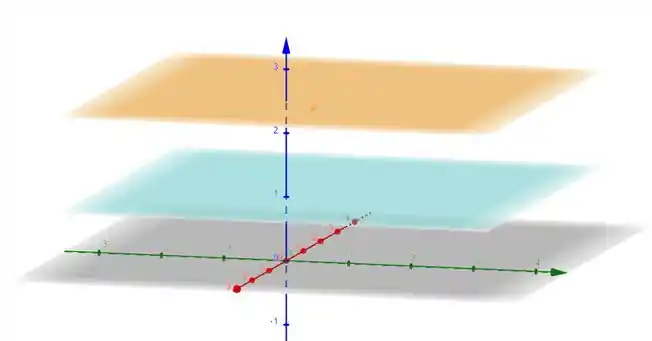
Agora vamos representar essas curvas de níveis.

f 1,1 = 1

f 1 , - 2 = f - 2 , - 1 = 5 2

Assim, teremos as seguintes curvas:

z = 1 e z = 5 / 2

Logo,

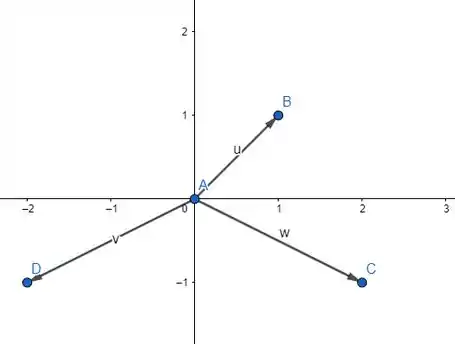
Passo 4

Para finalizarmos, vamos traçar os vetores ∇ f 1,1 , ∇ f 1 , - 2   e   ∇ f - 2 , - 1 . Lá da teoria a gente sabe o seguinte:

∇ f x , y = ∂ f ∂ x i → + ∂ f ∂ y j →

Assim,

∇ f x , y = ∂ 1 2 x 2 + 1 2 y 2 ∂ x i → + ∂ 1 2 x 2 + 1 2 y 2 ∂ y j →

Derivando parcialmente, temos:

∇ f x , y = 2 × 1 2 x   i → + 2 × 1 2 y   j →

Cortando o 2 :

∇ f x , y = x   i → + y   j →

Passo 5

Como já achamos a expressão de ∇ f x , y basta substituirmos os valores de x e y para encontrarmos os vetores pedidos.

Para ∇ f 1 , 1 :

∇ f 1,1 = 1   i → + 1   j →  

Para ∇ f 1 , - 2 :

∇ f 1 , - 2 = 1   i → - 2   j →

E para   ∇ f - 2 , - 1 :

∇ f - 2 , - 1 =   - 2   i → - 1   j →

Representando esses vetores, temos:

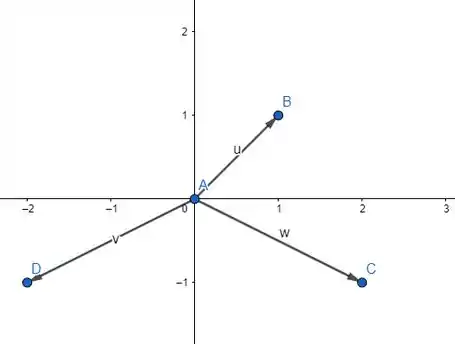
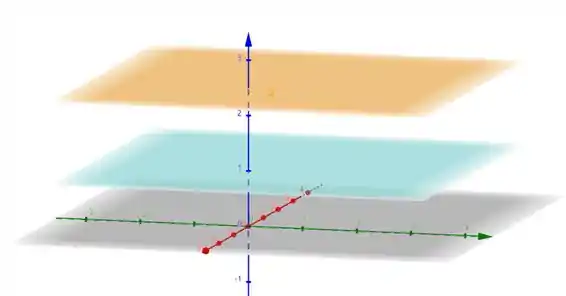
Resposta

Curvas de níveis:

Vetores:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

37. Mostre que a operação de calcular o gradiente de uma função tem a propriedade fornecida. Suponha que u e v sejam funções de x e y diferenciáveis, e a e b sejma constantes. ∇ a u + b v =a ∇ u + b ∇
Se f x , y = x y , encontre o vetor gradiente ∇ f 3,2 e use-o para encontrar a reta tangente à curva de nível f x , y = 6 no ponto 3,2 . Esboce a curva de nível, a reta tangente e o vetor gradiente