Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 95

Traçar num mesmo sistema de coordenadas as funções y = - 1 - x 2 e y = 1 + x 2 .Usando a visualização gráfica, responder:

  1. Quantas são as retas tangentes a ambas as parábolas?
  2. Quais são os pontos de tangência?
  3. É possível encontrar essas retas algebricamente?

Passo 1

Vamos ver os gráficos das funções primeiro...

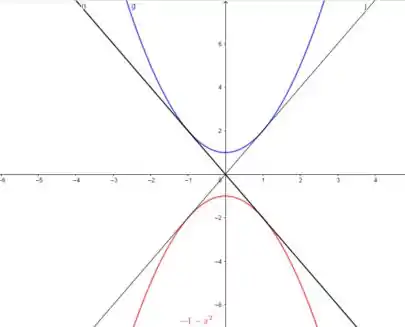
  1. Como podemos ver pelo gráfico, temos duas retas tangentes que são comuns aos dois gráficos.

    2. Passo 2

  2. Vemos pelo gráfico que os pontos de tangência são onde x = ± 1 , e que as funções são simétricas, então temos os pontos:

    3. P 1 : 1 ,   2   e   P 2 : ( - 1 , - 2 )

    P 3 : - 1,2   e     P 4 : ( 1 ,   - 2 )

    Passo 3

  3. Algebricamente falando, a gente faz as derivadas das funções:

f ' x =   - 2 x

g ' x = 2 x

Considerando os pontos P 1 : x 1 ,   y 1 e P 2 : ( x 2 ,   y 2 ) , sendo que pela figura vemos que x 2 = - x 1 e y 2 = - y 1 .

Aí montando a equação da reta tangente em P 1 :

y - y 1 = 2 x 1 x - x 1

Substituindo agora no ponto P 2 :

- y 1 - y 1 = 2 x 1 - x 1 - x 1

- 2 y 1 = 2 x 1 - 2 x 1

- 2 y 1 =   - 4 x 1 2

y 1 = 2 x 1 2

Como esses pontos pertencem às funções, vamos substituir isso na equação da função:

g x =   1 + x 2

2 x 1 2 = 1 + x 1 2

x 1 2 = 1

x 1 = ± 1

Encontramos os valores de x nas retas tangentes então. E daí vemos que os valores de y são y = ± 2 .

Com esses pontos, escrevemos as equações das retas tangentes:

  • (1,2) e (-1, -2): y - 2 = 2 1 ( x - 1 )

y = 2 x - 2 + 2

y = 2 x

E, por simetria, a outra é y = - 2 x .

Resposta

  1. Duas.
  2. 1,2 ,   - 1,2 ,   - 1 , - 2 ,   ( 1 ,   - 2 )
  3. y = 2 x e y = - 2 x .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre (d y)/(d x) :y = l n ( cos (e^x) )
Encontre (d y)/(d x) :y = e^(( x - e^(3 x) ))
Encontre (d y)/(d x) usando qualquer método:y = (x^3 - 2 x^2 + 1) e^x
Encontre f ' ( x ) pela Fórmula (7) e, então, por derivação logarítmica: f x = π x . t g ( x )
Encontre (d y)/(d x) :y = l n ( 1 - x e^(- x) )