Trace o gráfico da função e observe onde ela é descontínua. Em seguida, utilize a fórmula para explicar o que você observou.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função de duas variáveis:
Queremos traçar o seu gráfico e verificar onde ela é descontínua.
Em seguida, queremos comparar a figura com o gráfico para analisarmos a descontinuidade.
Agora bora lá!! 😉
Passo 2
Show de bola, galera. Vamos dar uma olhada no gráfico da função em duas perspectivas:
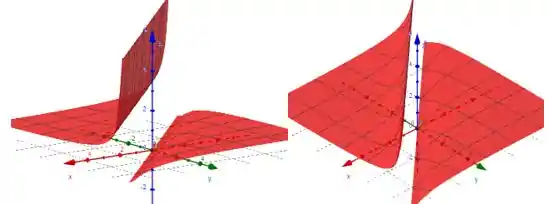
Parece que a função é descontínua ao longo da reta , certo?
De fato, se considerarmos uma função
E outra
Teremos que
Uma vez que é descontínua em , chegamos à correta conclusão de que a nossa função é descontínua em .
Resposta
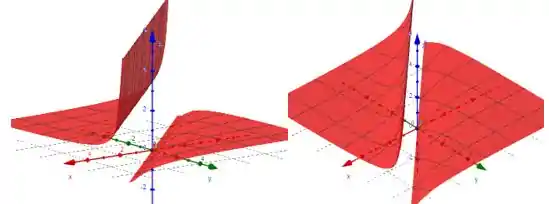
Descontinuidade em .