Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 24

Use coordenadas polares para determinar o volume do sólido dado.

Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e o plano z = 7 no primeiro octante.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão, precisamos encontrar o volume de um sólido limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 utilizando coordenadas polares. Então nosso processo de solução vai ser o seguinte:

  1. Escrever a função do parabolóide f ( x , y ) em f ( r , θ ) .
  2. Identificar os limites de integração, vendo onde o plano e o paraboloide se interceptam.
  3. Resolver a seguinte integral:

∬ D z d A

Em que z é a função do paraboloide e D é a região que o limita.

Mas antes disso, precisamos entender o que é primeiro octante.

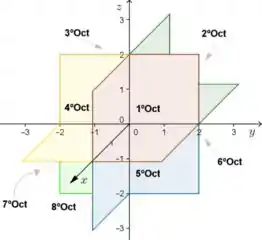
" 2 D " , o primeiro octante, também é a região no gráfico em que todas as coordenadas são positivas, porém, para gráficos de 3 coordenadas. (Ou seja, em “ 3 D ” ). Portanto é necessário que fique claro que iremos considerar apenas os valores positivos de cada eixo.

Passo 2

Em coordenadas retângulares, temos que a equação do paraboloide é dada por:

z = 1 + 2 x 2 + 2 y 2

Sendo assim, quando nos é dada a condição de que esse paraboloide é limitado pelo plano z = 7 , utilizamos essa informação para saber as coordenadas x e y que eles se interceptam.

7 = 1 + 2 x 2 + 2 y 2

Logo:

x 2 + y 2 = 3

Onde, escrevendo em coordenadas polares, temos as relações:

x = r cos ⁡ θ

y = r sen ⁡ θ

x 2 + y 2 = r 2

Então sabemos que x 2 + y 2 = r cos ⁡ θ 2 + r sen ⁡ θ 2 = r 2 , logo:

z = 1 + 2 x 2 + 2 y 2

Pode ser escrito como:

z = 1 + 2 r cos ⁡ θ 2 + 2 r sen ⁡ θ 2

E então:

z = 1 + 2 r 2 cos ⁡ θ + sen ⁡ θ 2

Das propriedades trigonométricas:

cos ⁡ θ 2 + sen ⁡ θ 2 = 1

Então temos:

z = 1 + 2 r 2

E sabendo que o paraboloide e o plano se interceptam em z = 7 .

7 = 1 + 2 r 2

6 2 = r 2

r = 3

Sabemos que o volume do sólido é dado por:

∬ D z d A

Lembe-se que estamos limitados ao primeiro octante, então θ não poderá ser > π 2 . Então a região D será a região delimitada por:

0 ≤ r ≤ 3 ,   0 ≤ θ ≤ π 2

Passo 3

Agora é só desenvolver. Como:

d A = r d r d θ

Lembrando que a equação do paraboloide é:

z = 1 + 2 r 2

E está limitado por z = 7

De modo que temos:

7 = 1 + 2 r 2

Manipulando:

7 - ( 1 + 2 r 2 )

Colocando na integral:

V = ∬ D z d A = ∫ 0 π / 2 ∫ 0 3 7 - 1 + 2 r 2 ⋅ r d r d θ

Simplificando e fazendo a distributiva com o r

V = ∫ 0 π / 2 ∫ 0 3 6 r - 2 r 3 d r d θ

Resolvendo a integral de dentro, temos:

∫ 0 3 6 r - 2 r 3 d r = 6 r 2 2 - 2 r 4 4 0 3

Aplciando os limites de integração:

1 2 6 3 2 - 3 4 =   1 2 18 - 9

9 2

Finalizada a integral “de dentro” temos que resolver a integral de “fora”:

Logo:

∫ 0 π / 2 ∫ 0 3 6 r - 2 r 3 d r d θ = ∫ 0 π / 2 9 2 d θ

Resolvendo, agora, temos:

∫ 0 π / 2 27 2 d θ = 9 2 θ 0 π / 2

Aplicando os limites de integração:

9 2 π 2   = 9 π 4

Portanto o volume vale:

V = 9 π 4

Resposta

V = 9 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando coordenadas polares, calcular:c) int_(- 1)^1 int_0^(sqrt(1 - x^2)) y d y d x
Usando coordenadas polares, calcular:d) int_0^1 int_0^(sqrt(y - y^2)) y d x d y
Usando coordenadas polares, calcular:i) int_0^2 int_0^(sqrt(2 x - x^2)) x d y d x
Usando coordenadas polares, calcular:e) int_(- 1)^1 int_(- sqrt(1 - x^2))^(sqrt(1 - x^2)) sqrt(1 - x^2 - y^2) d y d x
Usando coordenadas polares, calcular:h) int_0^a int_0^(sqrt(a^2 - x^2)) sqrt(x^2 + y^2) d y d x