Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.5 - Ex. 17
Use um diagrama de árvore para escrever a Regra da Cadeia em cada caso. Assuma que todas as funções são diferenciáveis.
onde e
Passo 1
Show de bola, galera! Questãozinha de regra da cadeia, vamos lá!
A questão nos dá uma função onde
Basicamente
E pede para que usemos um diagrama de árvore para nos ajudar a montar as derivadas parciais , e .
O diagrama é bem autoexplicativo. Nós vamos montar ele da função até cada uma das variáveis!
Passo 2
Se montarmos o diagrama das funções “de fora” para as “de dentro”, temos o seguinte:
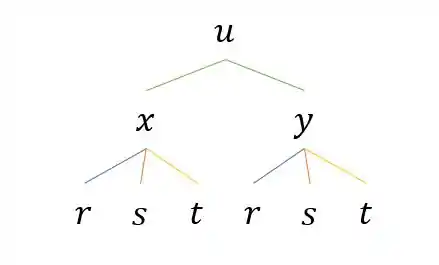
Em que, para montar a expressão de uma derivada parcial, por exemplo, nós percorremos os “galhos” que levam a da seguinte forma:
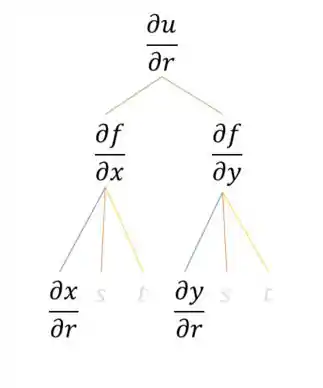
Onde por fim, podemos escrever
E da mesma forma para
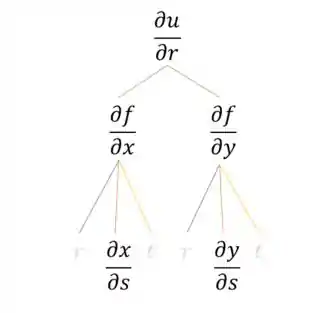
Onde podemos escrever
E por fim, para
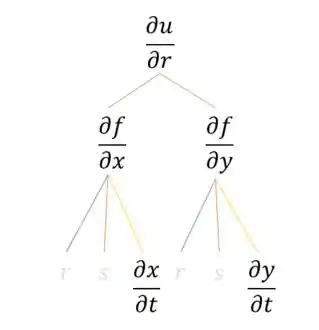
Onde podemos escrever