Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.5 - Ex. 18

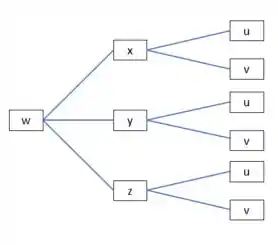
Use o diagrama em arvore para escrever a regra da cadeia para o caso dado. Assuma que todas as funções são diferenciáveis.

w = f x , y , z

Onde

x = x u , v

y = y u , v

z = z u , v

Passo 1

Oie, meu amigo. Tudo bem? Vou te ajudar a resolver essa atividade.

Basicamente a gente vai escrever a regra da cadeia aqui para todas as variáveis que existem em w , é isso que a questão quer.

Veja que ao aplicarmos a regra da cadeia, derivamos mais externamente para o mais interno. Isso é um pouco confuso mas iremos ver melhor com o desenho da arvore.

Mas lembre-se que, dada uma função w = f x , y , z , a derivada da função em relação a x , y , z onde as próprias variáveis são em função de outras variáveis, segue da seguinte forma:

w u = w x ⋅ x u + w y ⋅ y u + w z ⋅ z u

w v = w x ⋅ x v + w y ⋅ y v + w z ⋅ z v

Passo 2

Observe que, a partir da regra da cadeia acima, obteremos as derivadas parciais de w em relação a x , y e z . Portanto, ao fazer um diagrama em árvore, x , y e z estarão conectados a w . Além disso, estamos obtendo a derivada de x , y e z em relação a u e v . Portanto, u e v estarão conectados a x , y e z . Assim, o diagrama em árvore ficará assim.

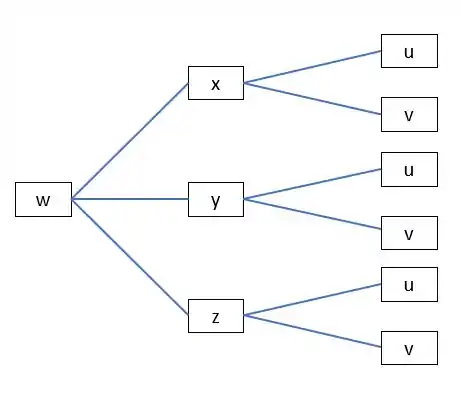
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que todas as funções dadas são diferenciáveis.Se z = f ( x , y ) , onde x = r cos ⁡ θ e y = r sen ⁡ θ , (a) determine ∂ z / ∂ r e ∂ z / ∂ θ e (b) mostre que ∂ z ∂ x 2 + ∂ z ∂ y 2 = ∂ z ∂ r 2 +
Use a Regra da Cadeia para achar (del z)/(del s) e (del z)/(del t) .7. z = x^2 y^3 , x = s cos t , y = s sen t
Use a regra da cadeia para achar ∂ z ∂ s e ∂ z ∂ t z = arcsin ⁡ x - y x = s 2 + t 2 y = 1 - 2 s t
Use a regra da cadeia para achar ∂ z ∂ s e ∂ z ∂ t z = sin ⁡ θ ⋅ cos ⁡ ϕ θ = s t 2 ϕ = s 2 t
Use a Regra da Cadeia para achar ∂ z ∂ s e ∂ z ∂ t . z = e x + 2 y x = s t y = t s