Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.6 - Ex. 5

Determine a derivada direcional de f no ponto dado e na direção indicada por θ

f x , y = y e - x ,             0,4 ,                     θ = 2 π 3

Passo 1

E aí, galera! Beleza?

Nesta questão o objetivo é descobrir qual é a derivada direcional no ponto ( 0,4 ) e na direção indicada pelo ângulo θ = 2 π / 3 .

A derivada direcional de f na direção de um vetor unitário u → é dada por:

D u f x , y = ∇ f x , y ⋅ u →

Portanto, precisamos calcular o gradiente da função f ( x , y ) e realizar o produto escalar dele com o vetor que dá a direção da derivada pedida.

Vamos ver como aplicar isso para a nossa questão...

Passo 2

Se a função é

f x , y = y e - x ,

o seu gradiente será

∇ f = ∂ f ∂ x x ^ + ∂ f ∂ y y ^

A primeira componente do gradiente, ∂ f ∂ x , é

∂ f ∂ x = ∂ ∂ x y e - x

∂ f ∂ x = - y ⋅ e - x

Enquanto a segunda é

∂ f ∂ y = ∂ ∂ y y e - x

∂ f ∂ y = e - x

Assim,

∇ f ( x , y ) = - y ⋅ e - x x ^ + e - x   y ^

No ponto dado, 0,4 , esse gradiente é

∇ f 0,4 =   - 4   x ^ +   y ^

Passo 3

Agora precisamos determinar o vetor unitário u → na direção de θ . Veja a figura abaixo um vetor que dá essa direção:

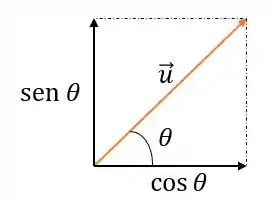
Note que ele é unitário, pois sen 2 ⁡ θ + cos 2 ⁡ θ = 1 .

Então, escreveremos u → como

u → = cos ⁡ θ   x ^ + sen ⁡ θ     y ^

Dessa forma, a direção do ângulo θ = 2 π / 3 é

u → = cos ⁡ 2 π 3     x ^ + sen ⁡ 2 π 3     y ^

u → = - 1 2 x ^ + 3 2   y ^

Passo 4

Agora que temos o gradiente da função no ponto dado e o vetor que dá a direção da derivada, podemos calcular a derivada direcional.

D u f 0,4 = ∇ f ( 0,4 ) ⋅ u →

D u f 0,4 = - 4   x ^ +   y ^ ⋅ - 1 2 x ^ + 3 2   y ^

Fazendo o produto escalar, obtemos

D u f 0,4 = 2 + 3 2

Resposta

2 + 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8. Encontre a derivada direcional de f x , y , z = x e y 2 - z 2 em P = ( 1,2 , - 2 ) na direção do vetor tangente σ ' t à curva σ t = ( t , 2 cos ⁡ ( t - 1 ) ,- 2 e t - 1 ) .
10. Uma chapa de metal aquecida está situada no plano x y de tal modo que a temperatura é inversamente proporcional à distância do ponto à origem. A temperatura em 3,4 é de 100 graus. Suponha que os e
11. As superfícies de equações: F x , y , z = x 2 + y 2 + z 2 - 3 = 0eG x , y , z = x 2 + 2 x + y 2 - 4 = 0 têm como interseção uma curva C que passa pelo ponto P 0 = ( 1,1 , 1 ) .b) Encontre a direçã
7- Considerando a função f x ,y = x 2 + y 2 - 2 y em P 0 = ( 2 ,2 ) . Determine:b)A taxa de variação de f em P 0 na direção do vetor tangente g ´ ( t ) à curva g t = ( t ,t 2 - t ) em ( 3 ,6 ) .
Nos exercícios 1 a 4, encontre a derivada direcional no ponto P 0 na direção do vetor u , nos seguintes casos:3- f x ,y ,z = ln ⁡ ( x 2 + y 2 + z 2 ) , P 0 = 1,2 ,3 ,u = ( 1 ,- 1 ,- 1 )