Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 65

Use a geometria ou simetria, ou ambas, para calcular a integral dupla.

Passo 1

E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!

Para resolver esta questão, primeiro precisamos entender o domínio da função, que é definido como um conjunto de valores de entrada onde a função está definida. Aqui, o domínio é descrito como:

Visualmente, essa região representa um semicírculo com raio centrado na origem, limitado pela curva no primeiro quadrante.

Passo 2

Abaixo, temos o esboço da região:

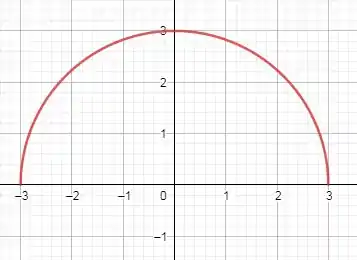
Passo 3

Nós temos que:

Sabemos que indica a área da região. Como a região é um semicírculo e a área do semicírculo é dada por , temos que:

Portanto, a integral de sobre a região é . Agora, considerando a função , que é ímpar em relação a dentro do intervalo , podemos concluir que a integral de sobre a região é zero, devido à simetria da função em relação ao eixo .