Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.3 - Ex. 38
Use o resultado do Problema 34 para encontrar a transformada de Laplace da função dada.
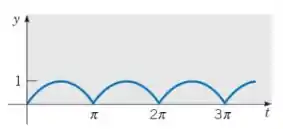
função , função seno retificada
Passo 1
Para uma função que se repete periodicamente a cada unidade T, a transformação Laplace é:
Passo 2
Nesse problema, o período é .
Use a integração por partes duas vezes para avaliar a integral no numerador.
Resolvendo a integral, chegamos em:
Passo 3
Como um resultado, temos:
E portanto, a equação se torna:
Resposta
Exercícios de Livros Relacionados
Encontre a transformada de Laplace da função dada. f ( t ) = 1-u 1 ( t ) + . . . + u 2 n ( t ) - u 2 n + 1 ( t ) = 1 + ∑ k = 1 2 n + 1 ( - 1 ) k u k ( t )
Encontre a transformada de Laplace da função dada. Suponha que é permitido integrar a série infinita termo a termo. f ( t )=1 + ∑ k = 1 ∞ ( - 1 ) k u k ( t ) função f ( t )
Se f ( t ) = 1 - u 1 ( t ) , encontre ℒ { f ( t ) } ; compare com o Problema 30. Esboce o gráfico de y =f(t).Seja g ( t ) = ∫ 0 t f ( ζ ) d ζ , em que a função f está definida em (a). Esboce o gráfico
Em cada um dosproblemas de 19a 24, encontre a transformada de Laplace inversa da função dada. F s = 2 ( s - 1 ) e - 2 s s 2 - 2 s + 2
Em cada um dosproblemas de 13a18, encontre a transformada de Laplace da função dada. f t = u 2 t t - 3 - u 3 t ( t - 2 )